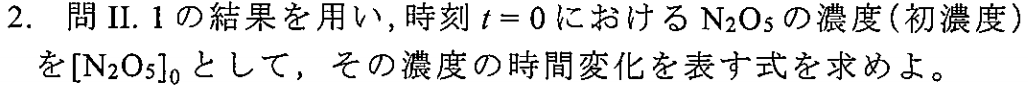$\newcommand\nn{[{\rm N_2O_5}]}
\newcommand\noo{[{\rm NO_2}]}
\newcommand\no{[{\rm NO}]}
\newcommand\nooo{[{\rm NO_3}]}
\newcommand\ka{k_{\rm 1}}
\newcommand\kaa{k_{\rm 2}}
\newcommand\kb{k_{\rm 3}}
\newcommand\kc{k_{\rm 4}}
$
$$\b
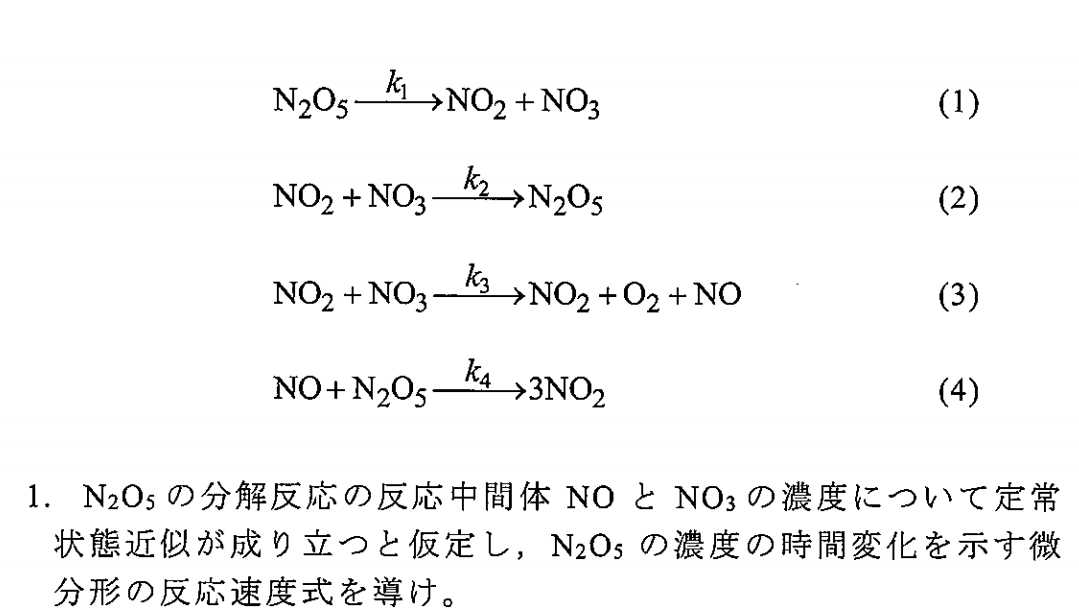
\df{\no}{t}&=&\kb\noo\nooo-\kc\no\nn\\
\df{\nooo}{t}&=&\ka\nn-\kaa\noo\nooo-\kb\noo\nooo\\
\e $$$$\df{\nn}{t}=-\ka\nn+\kaa\noo\nooo-\kc\no\nn\tag{☆}\\$$ 定常状態近似より、
$$\b
\df{\no}{t}&=&\kb\noo\nooo-\kc\no\nn=0\tag1\\
\df{\nooo}{t}&=&\ka\nn-\kaa\noo\nooo-\kb\noo\nooo=0\tag2\\
\e$$ $(1)$式より
$$\no\nn=\f{\kb}{\kc}\noo\nooo\tag3$$ $(3)$式を$(☆)$式に代入
$$\df{\nn}{t}=-\ka\nn+\kaa\noo\nooo-\kb\noo\nooo\tag{★} $$$(2)$式より
$$\noo\nooo=\f{\ka}{\kaa+\kb}\nn\tag4 $$$(4)$式を$(★)$式に代入すると、
$$\df{\nn}{t}=\left(-\ka+\f{\ka\kaa}{\kaa+\kb}-\f{\ka\kb}{\kaa+\kb}\right)\nn $$となる。
$\left(-\ka+\f{\ka\kaa}{\kaa+\kb}-\f{\ka\kb}{\kaa+\kb}\right)=-K$と置くと、
$$\df{\nn}{t}=-K\nn$$となる。
$$\b
\df{\nn}{t}&=&-K \\
\df{\nn}{\nn}&=&-K\d t \\
&&積分すると \\
\ln{\nn}&=&-Kt+C \\
&&(Cは積分定数) \\
C&=&\ln{\nn_0} \\
&& (\because 初期条件より)\\
\ln{\nn}&=&-Kt+\ln{\nn_0} \\
\ln{\f{\nn}{\nn_0}}&=&-Kt \\
\f{\nn}{\nn_0}&=& e^{-Kt}\\
\nn&=&\nn_0e^{-Kt} \\
\e$$ となる。
$\newcommand\c{C_{\rm V}}$
熱力学第一法則より
$$\b
\d U&=&δQ+δW \\
\d U&=&δW \\
&&(\because 断熱過程においてδQ=0) \\
C_{\rm V}\d T&=&-P\d V \\
\c\d T&=&-\f{nRT}{V}\d V \\
\c\f{1}{T}\d T&=&-\f{nR}{V}\d V \\
\c\int^{T_H}_{T_L}\f{1}{T}\d T&=&-nR\int^{0.8V}_{V}\f{1}{V}\d V \\
&&(初期状態の体積をV、温度をT_L、終状態の温度をT_Hとした) \\
\c\ln{\f{T_H}{T_L}}&=&nR\ln{\f{0.8V}{V}} \\
\ln{\f{T_H}{T_L×0.8}}&=&\f{nR}{\c} \\
T_H&=&T_L×0.8×\exp{\f{nR}{\c}}\\
&=& 367×0.8×\exp{\f{1.0×8.31}{20.74}}\\
&=&438.29\\
&=&438[{\rm K}]
\e$$
 この問題は回答作成中です。
この問題は回答作成中です。この問題の解説