等温定圧下では平衡定数$K$は$ΔG$ではなく、$ΔG\stst$と密接に関係しています。つまり、平衡定数$K$は$ΔG\stst$が分かっていれば、簡単に求めることができるということです。しかし、実際の化学の現場では、平衡定数$K$は$ΔG\stst$から求められることはほとんどありません。より直接的なデータである$ΔH\stst$から求めることができるからです。逆に、異なる温度における平衡定数$K$を複数点求めることで、$ΔH\stst$を求めることもしばしばです。この平衡定数$K$と$ΔH\stst$をつなげる式をファント・ホッフの式と言います。
\begin{eqnarray}
ΔG\stst&=&-RT\ln K_{\rm p} \\
両辺をTで割って&、& \\
\f{ΔG\stst}{T}&=&-R\ln K_{\rm p} \tag{1} \\
ここで、ギブズ-ヘルムホルツの式より&、& \\
\m{\ddp{}{T}\s{\f{ΔG\stst}{T}}}_{\rm P}&=&-\f{ΔH\stst}{T^2}\tag{2} \\
いまΔG\ststを考えているので&、&各成分気体の分圧はすべて{\rm 1bar} \\
したがって、全圧も一定であることから&、&ギブズヘルムホルツの式を用いる \\
条件であるP&=&一定を満たしています。よって、 \\
(1)式を(2)式に代入すると&、& \\
\m{\ddp{}{T}-R\ln K_{\rm p}}_{\rm P}&=&-\f{ΔH\stst}{T^2}\\
-R\m{\ddp{}{T}\ln K_{\rm p}}_{\rm P}&=&-\f{ΔH\stst}{T^2}\\
\m{\ddp{\ln K_{\rm p}}{T}}_{\rm P}&=&\f{ΔH\stst}{RT^2}\\
\end{eqnarray}
となります。この式がファント・ホッフの式です。
(浸透圧に関するファント・ホッフの式もありますので、紛らわしいですね・・・(笑))
ここで、気体定数$R$は正の定数、温度$T$は絶対温度でありますので、符号は正であります。そのため、このファント・ホッフの式から以下のことが言えます。
(1)吸熱反応($ΔH\stst>0$)のとき平衡定数$K_{\rm P}$の温度依存性は正になります。すなわち、温度が上昇するほど$K_{\rm P}$が増加します。
(2)発熱反応($Δ\stst<0$)のとき平衡定数$K_{\rm P}$の温度依存性は負になります。すなわち、温度が上昇するほど$K_{\rm P}$が減少します。
少しながながと書いてしまいましたが、つまりこれはルシャトリエの原理に従う、ごく当たり前な結論です。
(1)ある反応の平衡定数を、温度$T_1$と$T_2$において、それぞれ$K_{P_1}$、$K_{P_2}$とする。この反応の反応熱$ΔH\stst$と$T_1$,$T_2$,$K_{P_1}$、$K_{P_2}$の関係式を示せ。ただし、$ΔH\stst$は温度によらず一定としても良い。
(2)$\rm NH_3$の生成反応の平衡定数$K_p$は、温度350℃と450℃においてそれぞれ$26.6×10^{-3}$と$6.59×10^{-3}$である。(1)で求めた関係式から反応熱を求め、さらにそれを用いてファント・ホッフプロット(傾きがわかる定性的な図)を示せ。また、発熱反応であるか、吸熱反応であるか答えよ。
$$\rm \f12N_2+\f32H_2→NH_3 $$
解答
(1)ファント・ホッフの式より
$$\b
\ddp{\ln K_P}{T}_P&=&\f{ΔH\stst}{RT^2} \\
\d \ln K_p&=&\f{ΔH\stst}{RT^2} \d T\\
このとき、\f{\d \frac1T}{\d T}&=&-\f{1}{T^2}であるから、 \\
\d \s{\f1T}&=&-\f{1}{T^2}\d T である。よって、\\
\d \ln K_p&=& -\f{ΔH\stst}{R} \d \s{\f1T}\\
&&積分すると、ΔH\ststは定数とみなせるので、\\
\int_{\ln K_{P_1}}^{\ln K_{P_2}}\d \ln K_p&=& -\f{ΔH\stst}{R}\int^{T_2}_{T_1} \d \s{\f1T}\\
\ln K_{P_2}-\ln K_{P_1}&=&-\f{ΔH\stst}{R}\s{\f1{T_2}-\f{1}{T_1}} \\
\e $$となる。
(2)
$$\b
\ln K_{P_2}-\ln K_{P_1}&=&-\f{ΔH\stst}{R}\s{\f1{T_2}-\f{1}{T_1}} \\
&&この式にあたえられた数値を代入すると、 \\
\ln \s{26.6×10^{-3}}-\ln \s{6.59×10^{-3}}&=&-\f{ΔH\stst}{8.3145}(\f{1}{623}-\f{1}{723}) \\
\ln \f{26.6×10^{-3}}{6.59×10^{-3}}&=&-\f{ΔH\stst}{8.3145}(\f{1}{623}-\f{1}{723}) \\
ΔH\stst&=&-53.3[{\rm kJ \ mol^{-1}}] \\
\e $$となる。よって、ファント・ホッフプロットは以下のようになる。
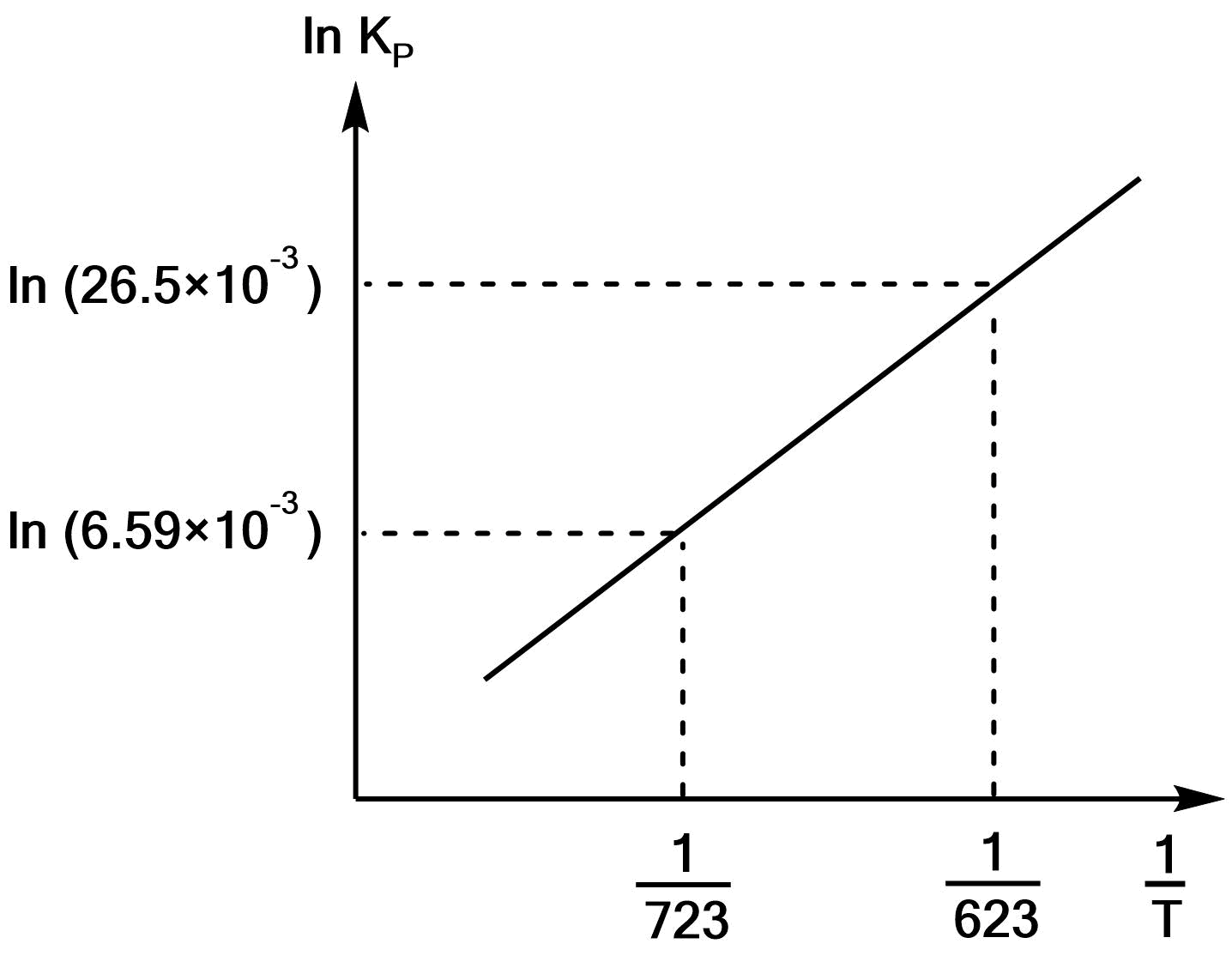
また、この反応は$ΔH\stst$が負なので、発熱反応である。
引用)由井 宏治 化学熱力学入門 p198