$\newcommand\E{[{\rm E}]}\newcommand\S{[{\rm S}]}\newcommand\P{[{\rm P}]}\newcommand\ES{[{\rm ES}]}$
ミカエリスメンテン機構は$\rm S+E⇄ES$と$\rm ES→P+E$の二つの反応過程で説明されます。
※このページでは、基質を$\rm S$(substrate)、酵素を$\rm E$(enzyme)、酵素基質複合体を$\rm ES$、生成物を$\rm P$(Product)と表記します。
$\rm S+E⇄ES$は、基質と酵素と酵素基質複合体との平衡反応のことです。つまり、酵素の活性サイトに基質が入りこみ、酵素基質複合体になったり、その酵素基質複合体で何の反応も起きず、元の基質と酵素に分解してしまうという平衡反応のことです。
$\rm ES→P+E$は酵素基質複合体で、何らかの反応が起こり、基質が生成物に変化し、その後、酵素基質複合体が生成物と酵素に分解するという反応です。
以下では、はじめの平衡反応$\rm S+E⇄ES$の正反応をStep1,逆反応をStep2、
$\rm ES→P+E$という反応をStep3として、ミカエリスメンテンの式の導出を行っていきたいと思います。
Step1酵素と基質が出会って、酵素基質複合体$\rm ES$を形成する
$$\rm E+S\overset{ k_a}{→ }ES(反応速度はk_a)$$
Step2酵素基質複合体からもとの酵素と基質に分解する(Step1の逆反応)
$$\rm E+S\underset{ k’_a}{← }ES(反応速度はk’_a)$$
Step3反応が起こり、酵素基質複合体から、生成物と酵素になる。
$$\rm ES\overset{ k_b}{ →}P+E(反応速度はk_b)$$
です。
ここで、知りたいのは、${\rm P}$の生成速度であります。
ミカエリス・メンテンの速度式はこの${\rm P}$を求める式です。
以下ではミカエリス・メンテンの速度式の導出をしていきます。
定常状態近似法をつかいますが、この場合、中間体は明らかに${\rm ES}$です。
${\rm ES}$の生成速度を考えます。${\rm ES}$は中間体なので、定常状態近似を用いることができます。
$$\b
\f{\d \ES}{\d t}&=&k_a\E\S-k’_a\ES-k_b\ES=0(定常状態近似) \\
\ES&=&\f{k_a\E\S}{k’_a+k_b}\tag{1}
\e $$$\Eと\S$は遊離の(結合していない)酵素と基質の濃度のことを指します。
酵素の全濃度を$\E_0$とすると、
$$\b
\E+\ES&=&\E_0 \\
\E&=&\E_0-\ES \\
\e$$これを$(1)$式に代入すると、
$$\b
\ES&=&\f{k_a\s{\E_0-\ES}\S}{k’_a+k_b} \\
&&これを更に\ESについて解いていきます\\
k’_a\ES+k_b\ES&=&k_a\E_0\S-k_a\ES\S \\
\s{k_a+k_b+k_a\S}\ES&=&k_a\E_0\S \\
&&両辺をk_aで割ると\\
\s{\f{k’_a+k_b}{k_a}+\S}\ES&=&\E_0\S \\
\f{k’_a+k_b}{k_a}&=&K_Mとすると、 \\
\s{K_M+\S}\ES&=&\E_0\S\\
\ES&=&\f{\E_0\S}{\S+K_M}\tag{2}
\e $$となります。この$K_M=\f{k’_a+k_b}{k_a}$はミカエリス定数といって、濃度の次元を持ちます。なぜなら、$k’_a+k_b$は一次反応における反応速度定数で、$k_a$は二次反応における反応速度定数だからです。
よって、
$$\b
Pの生成速度&=&k_b\ES \\
&=&\f{k_b\E_0\S}{\S+K_M} ((2)式を代入)\\
k_r&=&\f{k_b\S}{\S+K_M}とおくと、\\
&=& k_r\E_0\\
\e$$ となります。
つまり、Pの生成速度は加えた酵素の濃度に比例することがわかります。
$\S<<K_M$のとき、つまり、基質の濃度が小さいときは、
$$k_r≒\f{k_b\S}{K_M} となります。
つまり、基質の濃度が小さい場合は、
$\S$に対して、$k_r$が直線的に増加します。
$\S>>K_M$のとき、つまり、基質の濃度が大きいときは、
$Pの生成速度=k_b\E_0$
となります。つまり、これ以上基質を加えても、Pの生成速度が増えないことがわかります。
この速度を$v_{\rm max}$とおくと、
$$v_{\rm max}=k_b\E_0 $$となります。つまり、とても基質の濃度が十分大きいこの条件では、律速段階がStep3であるということです。
よって、$v_{\rm max}=k_b\E_0$ですので、
$$v(=Pの生成速度)=\f{\S v_{\rm max}}{\S+K_M}\tag{*}$$ 書き直すことができます。
グラフの概形は以下のようになります。
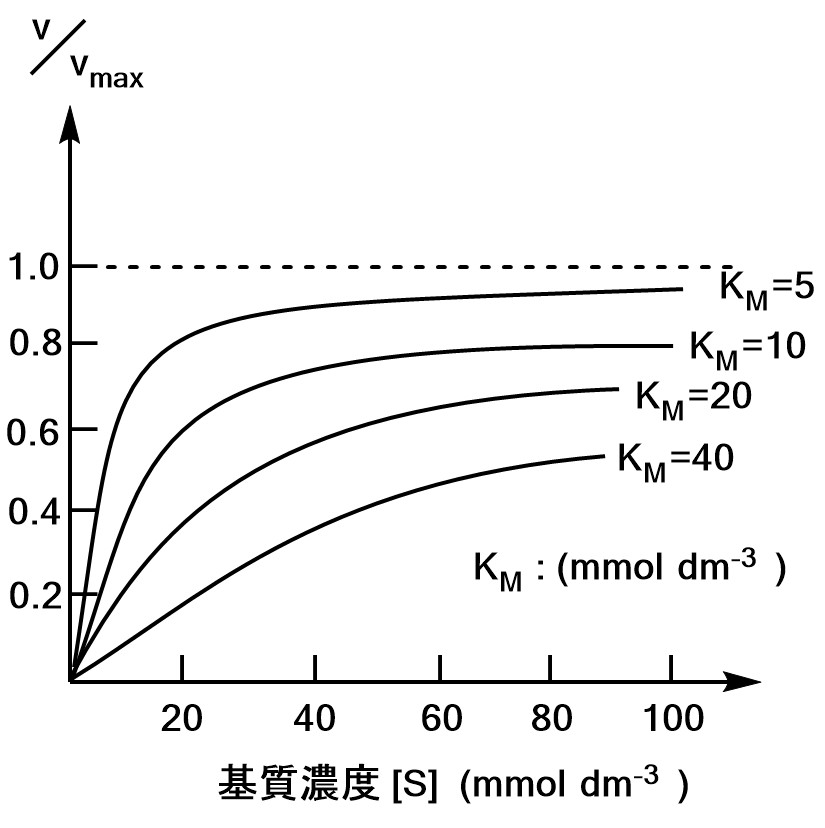
まとめると、
・$K_M$が小さい⇔${\rm ES}$ができやすい。
・$\S<<K_M$では$v∝\S$
・$\S>>K_M$では$v$は$\S$に依存しない
ということがわかります。
またこれでは終わりません。$(*)$式の逆数をとると、
$$\b
\f{1}{v}&=&\s{\S+K_M}{\S v_{\rm max}} \\
&=&\f{1}{v_{\rm max}}+\s{\f{K_M}{v_{\rm max}}}×\f{1}{\S} \\
y&=&切片+勾配×x \\
\e$$ の関係が成り立つことがわかります。つまり、実験から得られた数点のプロットから$v_{\rm max}$を求めることができるということがわかります。
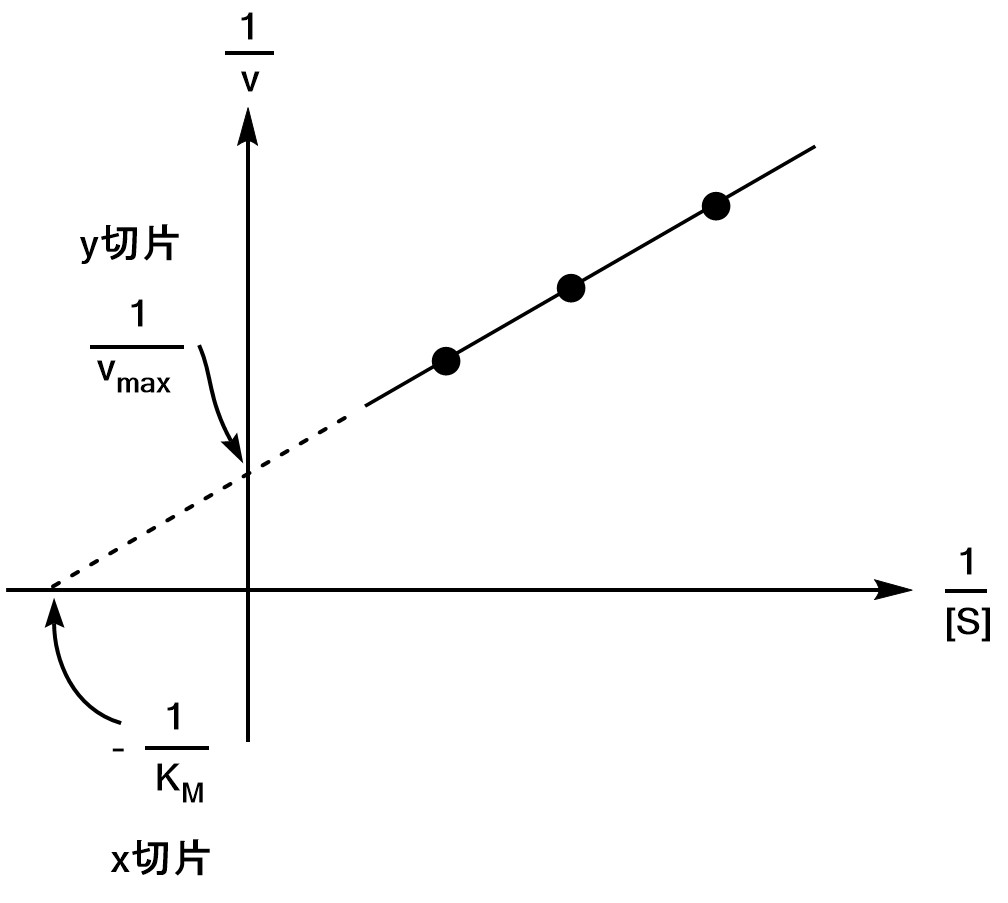
このグラフをラインウィーバー・バークプロット(Lineweaver-Burk plot)といいます。
以下はラインウィーバー・バークプロットの例題です。
例題)
ある酵素反応に関して以下のようなデータを得た。
基質濃度を 1,2,5,10 mM とした時の反応速度を測定したところ,それぞれ 5.0,8.0,12.5,15.4 μM/s という値が得られた。
これより、ミカエリス定数$K_M$と最大の反応速度$v_{\rm max}$を求めよ。
解答)
ラインウィーバー・バークプロットをエクセルで描くと以下のようになり、点をつなげた直線式は$y=0.15x+0.05$となります。
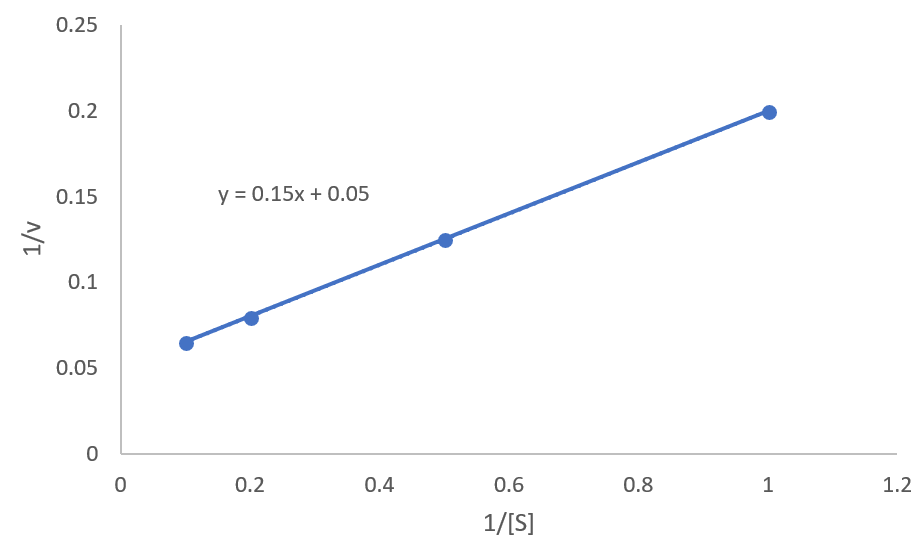
これより、y切片は0.05であることがわかります。次はx切片です。この式に$y=0$を代入すれば、$x=-1/3$と出てきます。よって、
$$\b
-\f{1}{K_M}&=-\f13& \\
\f1{v_{\rm max}}&=&0.05=\f1{20} \\
\e $$となるため、
$$\b
K_M&=&3 .0\\
v_{\rm max}&=&20 \\
\e $$となります。
(※問題に合わせてデータを作りましたので、きれいな値になっています。)
ミカエリスメンテンは酵素阻害については説明していません。
簡単に酵素阻害について説明します。
酵素の阻害には大きく二種類があります。
・拮抗阻害(きっこうそがい)
基質は酵素の活性サイトに入り込む必要がありますが、基質とよく似た形の阻害剤がある場合、基質ではなく、形のよく似た阻害剤が入り込んでしまう場合があります。
・非拮抗阻害(ひきっこうそがい)
非拮抗阻害は阻害剤は活性サイトには入り込みませんが、活性サイト以外と結合することで、活性サイトが歪んでしまい、基質が結合できなくなります。
この間接的阻害を非拮抗阻害といいます。
実際の反応では、このような阻害も考える必要がある場合もあります。あくまで、ミカエリス・メンテンの式はこのような阻害は考えていないことに留意する必要があります。