H26の問題はこちら
 解答
解答
Ⅰ-(1)(2)
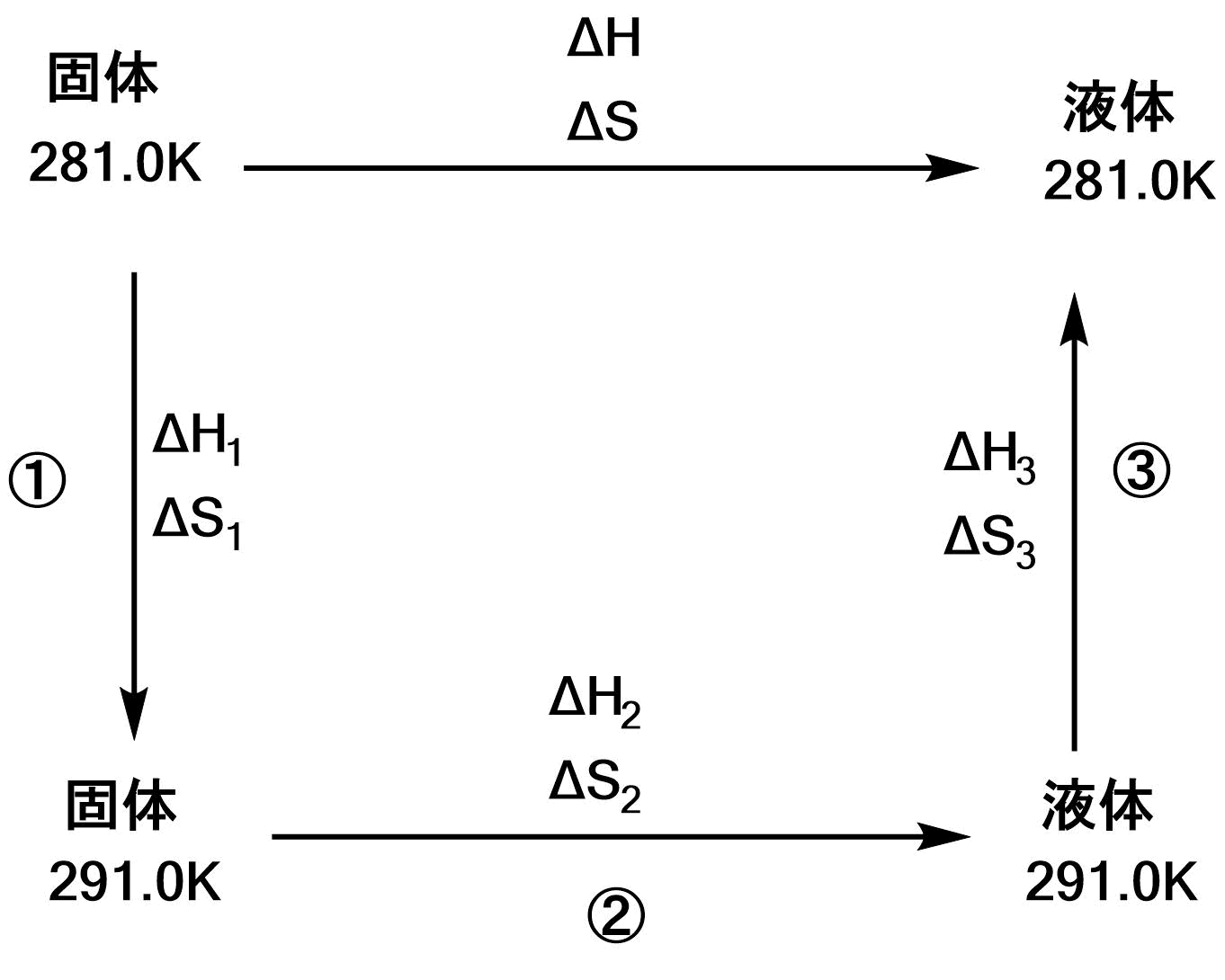
$ΔH=ΔH_1+ΔH_2+ΔH_3$、$ΔS=ΔS_1+ΔS_2+ΔS_3$である。
過程①において、
$$\b
ΔH_1&=&\int_{281.0}^{291.0}C_{固体}\d t \\
&=& 94.30×10\\
&=& 943.0[J \ mol^{-1}]\\
ΔS_1&=&\int_{281.0}^{291.0}\f{C_{固体}}{T}\d t \\
&=&94.30×\ln\s{\f{291.0}{281.0}}
&=&94.30×0.0349
&=&3.29[{\rm J \ K^{-1}}]
\e $$過程②において、
$$\b
ΔH_2&=&-11.60 [kJ \ mol^{-1}]\\
ΔS_2&=&\f{-11.60×1000}{291}\\
&=&-39.86[{\rm J \ K^{-1}}]\\
\e $$過程③において、
$$\b
ΔH_3&=&\int_{291.0}^{281.0}C_{液体}\d t \\
&=& -120.4×10\\
&=& -1204[J \ mol^{-1}]\\
ΔS_3&=&\int_{291.0}^{281.0}\f{C_{液体}}{T}\d t \\
&=&120.4×(-0.349)\\
&=&-4.210[{\rm J \ K^{-1}}]
\e $$
よって、
$$\b
ΔH&=& \f{943.0}{1000}-11.60- \f{1204}{1000}\\
&=& -\rm 11.86[kJ \ mol^{-1}]\\
ΔS&=&3.29-39.86-4.210\\
&=& 40.78[{\rm J \ K^{-1}}]
\e$$ である。
(3)
外界が得た熱量は$-ΔH=\rm 11.86[kJ \ mol^{-1}]$であるが、外界の熱容量は無限と考えていいので、温度は変化しない。
よって、外界のエンタルピー変化は、
$$ΔS_{外界}=\f{11.86×1000}{281.0}=42.20[{\rm J \ K^{-1}}]$$ であるので、
$$ΔS_{全体}=ΔS_{系}+ΔS_{外界}=-40.78+42.20=1.426[{\rm J \ K^{-1}}]>0$$ となるため、この反応は不可逆変化である。
 解答
解答
Ⅱ-(1)
$$\b
\rm β-Snの密度&=&\f{単位格子内の\rm Snの重さ}{単位格子の体積}\ \\
&=& \f{\rm 4×118.7[g \ mol^{-1}]÷6.022×10^{23}}{0.5832^2×0.3181×10^{-21}[{\rm cm^{3}}]}\\
&=& 7.28[{\rm g \ cm^{-3}}]\\
\e $$となる。
 解答
解答
Ⅱ-(2)
$G≡H-ST$より、等温過程において、$ΔG=ΔH-TΔS$である。
よって、
$$\b
ΔG\maru_{β→α}&=&Δ_{\rm trs}H-TΔS\maru_{β→α} \\
125.5&=&Δ_{\rm trs}H-298.2×(44.14-51.18) \\
Δ_{\rm trs}H&=&125.5-298.2×7.04 \\
&=&-1.97×10^{3}[{J \ mol^{-1}}] \\
\e $$となる。

解答
Ⅱ-(3)
※$U≡U+PV、G≡H-TS$から始めるととても長い回答になりますし、この式以外にも、$dS≡\f{δQ_{\rm rev}}{T}、\d U=δQ+δW$の二式も必要になるので、熱力学の基本式$\d G=V\d P-S\d T $は使用してもいいとします。(もちろん余裕があれば、この熱力学の基本式から出す方がもちろんいいでしょう。)
1molあたりのα相とβ相のギブズエネルギーをそれぞれ$G_{\rm α},G_{\rm β}$とすると、2つの相が平衡状態に達しているので、
$$\b
\d G_{\rm α}&=&\d G_{\rm β} が成り立つ。よって、\\
V_{\rm α}\d P-S_{\rm α}\d T&=&V_{\rm β}\d P-S_{\rm β}\d T \\
(V_{\rm α}-V_{\rm β})\d P&=&(S_{\rm α}-S_{\rm β})\d T \\
Δ_{\rm trs}V\d P&=&Δ_{\rm trs}S\d T \\
\f{\d P}{\d T}&=&\f{Δ_{\rm trs}S}{Δ_{\rm trs}V}\tag{1} \\
\e $$となる。また、平衡が成り立つならば、
$$\b
Δ_{\rm trs}G&=&0が成り立つので\\
Δ_{\rm trs}H-TΔ_{\rm trs}S&=&0\\
Δ_{\rm trs}S&=&\f{Δ_{\rm trs}H}{T} \tag{2}\\
\e $$$(2)式を(1)式$に代入すると、式$[1]$であるクラペイロンの式
$$\f{\d P}{\d T}=\f{Δ_{\rm trs}H}{TΔ_{\rm trs}V}$$ が得られる。
 解答
解答
Ⅱ-(4)
$$\b
Δ_{\rm trs}V&=&V_{α}-V_{β} \\
&=& \f{118.7[{\rm g \ mol^{-1}}]}{5.679×10^6[{\rm g \ m^{-3}} ]}-\f{118.7[{g \ mol^{-1}}]}{7.28×10^6[{g \ m^{-3}}]}\\
&=& 4.569×10^{-6}[{\rm m^3}]\\
\e $$
よって、相図における傾きは、
$$\b
\f{\d P}{\d T}&=&\f{Δ_{\rm trs}H}{TΔ_{\rm trs}V} \\
&=& \f{-1.97×10^{3} }{286.4×4.569×10^{-6}}\\
&=& -1.505×10^6\\
\e $$
となる。
![]() 解答
解答
Ⅱ-(5)
相図の傾きが負なので、圧力を上昇させた時、相平衡温度は286.4℃より低下する。