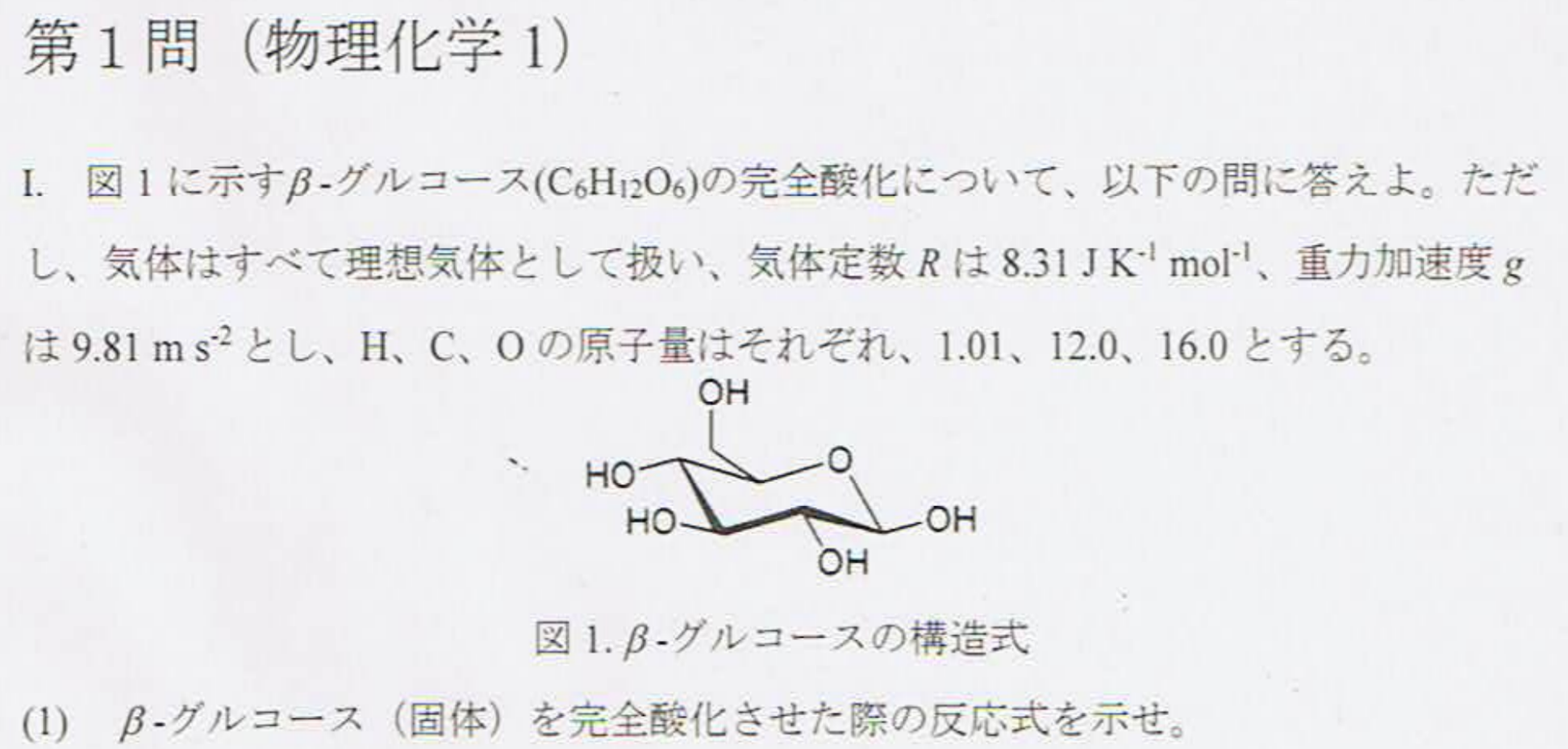
$$\rm C_6H_{12}O_6+6O_2→6CO_2+6H_2O$$
β-グルコースを成分原子からつくるための標準エンタルピー変化はβ-グルコースの結合エンタルピーの合計に等しい。よって、
$$\b
ΔH\maru&=&-(5ΔH\maru_{\rm C-C}+7 ΔH\maru_{\rm C-O}+5ΔH\maru_{\rm O-H}+7ΔH\maru_{\rm C-H})\\
&=& -(5×348+7×360+5×463＋7×412)\\
&=& -9459{[\rm kJ \ mol^{-1}]}\\
&=& -9.46×10^{3}{\rm [kJ \ mol^{-1}]}\\
\e$$
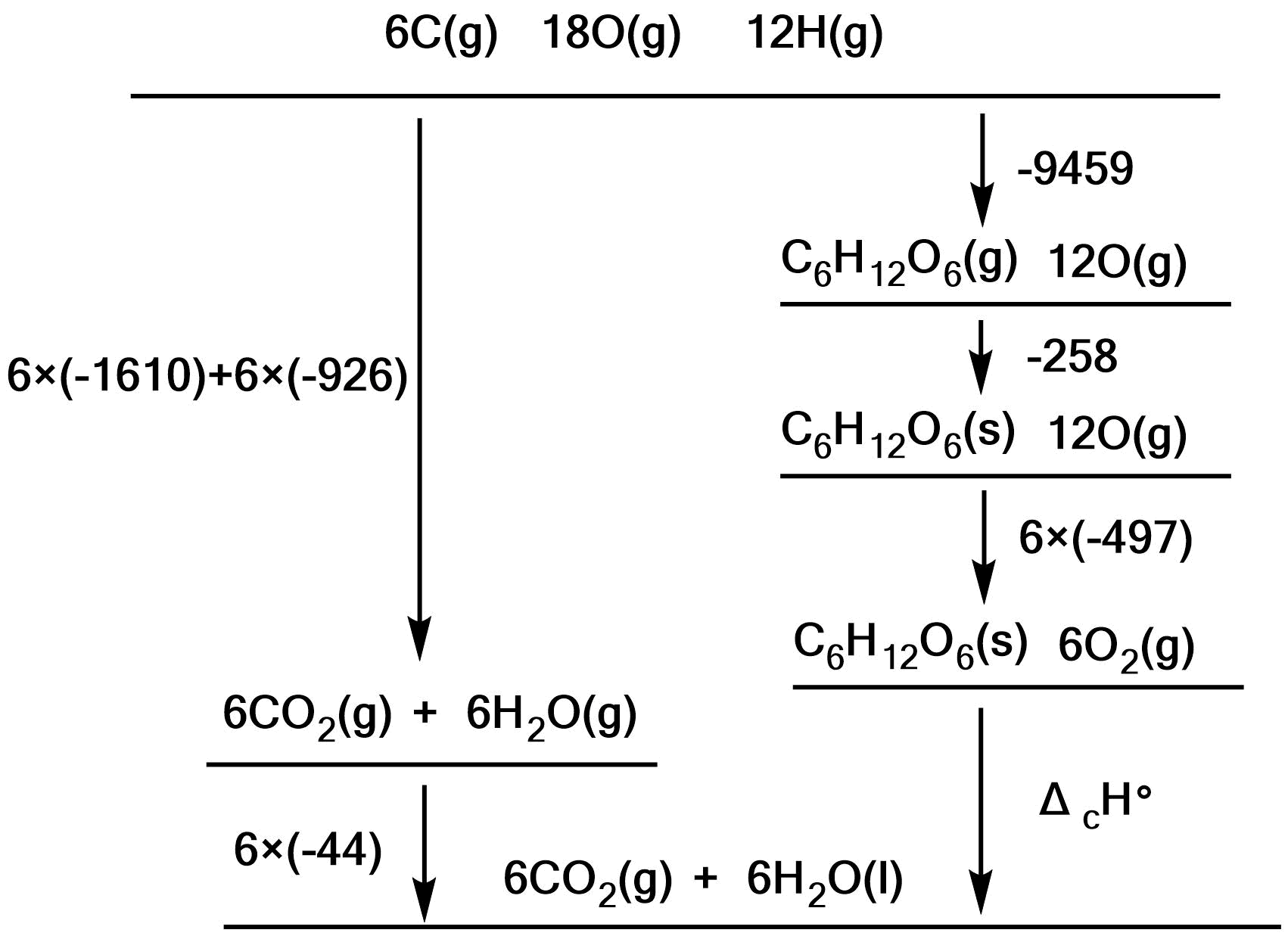
上の図より、
$$\b
ΔH_c\maru&=&(6×(-1610)+6×(-926)+6×(-44))-(-9459-258+6×(-497)) \\
&=&-2781[{\rm kJ \ mol^{-1}}] \\
&=& -2.78×10^{3}[{\rm kJ \ mol^{-1}}]\\
\e $$
標準状態におけるβ-グルコースの完全酸化の式は
$$\rm C_6H_{12}O_6(s)+6O_2(g)→6CO_2(g)+6H_2O(l)$$ となるため、液体や固体の体積変化は気体の体積変化と比べて無視できるとすると、
生成系と反応系の体積変化（並びに圧力変化）は0であると考えられる。
クラウジウスの式より、
$$\f{\d P}{\d T}=\f{Δ_cH}{TΔV}$$である。
液体や固体の体積変化は気体の体積変化と比べて無視できるとすると、
$$\b
\f{\d P}{\d T}&=& \f{Δ_cH}{TΔV_{\rm gas}}\\
\f{\d P}{\d T}&=& \f{Δ_cH}{T\frac{Δn_{\rm gas}RT}{P}}\\
Δn_{\rm gas}R\f{\d P}{P}&=&\f{Δ_cH}{T^2}\d T \\
&&ここで、両辺を生成系から反応系へ積分すると、 \\
Δn_{\rm gas}R\int^{P_{生成系}}_{P_{反応系}}\f1{P}\d P&=& \int^{310}_{298}\f{Δ_cH}T\d T\\
0&=&\l{\f{Δ_cH_{310K}}{310}-\f{Δ_cH\maru}{298}}(\because Δn_{\rm gas}=0)\\
Δ_cH_{310K}&=&Δ_cH\maru×\f{310}{298}\\
&=& -2892[\rm {kJ \ mol^{-1}}]\\
&=&-2.89×10^{3}[\rm {kJ \ mol^{-1}}]\\
\e$$ よって、310Kにおける内部エネルギー変化は
$$\b
Δ_{r}U\maru&=& Δ_cH_{310K}+PΔV\\
&=&Δ_cH_{310K}+0（\because ΔV=0） \\
&=&-2.89×10^{3}[\rm {kJ \ mol^{-1}}] \\
\e $$
また、ヘルムホルツの自由エネルギーの定義$A≡U=TS$より、310K下において、
$$\b
Δ_rA\maru&=&Δ_rU\maru-TΔ_cS\maru \\
&=& -2892-310×182×10^{-3}\\
&=& -2949.3[{\rm kJ \ mol^{-1}}]\\
&=&-2.95×10^3[{\rm kJ \ mol^{-1}}] \\
\e $$となる。
β-グルコースが$x[{\rm mol}]$消費されたとすると、
$$\b
-xΔ_rA\maru&=& mgh\\
x&=&\f{60×9.81×20}{2949×10^3} \\
&=& 3.991×10^{-3}\\
\e $$よって、必要なβ-グルコースの質量は、
$$3.991×10^{-3}×180=0.718[{\rm g}]$$ となる。
※310Kという標準状態ではない系において、標準状態の記号$\maru$を使用するのは本来推奨されませんが、解答では問題の表記にしたがい、310K下においても$\maru$を使用しております。また、この大問の標準解答時間は20分です。実際は、この時間内に上記のような丁寧な解答を制作するのは難しいと思われます。そのため、実際の試験では、ある程度、使用する式や方向性を示し、答えが正確に出せていれば、ほぼ満点に近い解答だと思います。
酸素分子について、$M=\f{32.0×10^3}{6.0×10^{23}}[{\rm kg}]$であるから、
$$\bar{c}=\sqrt{\f{8×1.4×10^{-33}×300}{π×\f{32.0×10^3}{6.0×10^{23}}}}=4.48×10^2{[\rm ms^{-1}]}$$
(2)理想気体の状態方程式から、
\begin{eqnarray}
N&=&\f{PV}{kT} \\
&=& \f{1.0×10^{-8}×10^{-6}}{1.4×10^{-23}×300}\\
&=& 2.38×10^6[{\rm 個}]\\
\end{eqnarray}
(3)
\begin{eqnarray}
Z_w&=&\int^{∞}_{0}N\sqrt{\f{m}{2πkT}}v\exp\s{-\f{mv^2}{2kT}}\d v \\
&=&N\sqrt{\f{m}{2πkT}} int^{∞}_{0}v\exp\s{-\f{mv^2}{2kT}}\d v\\
&=& N\sqrt{\f{m}{2πkT}}\f{1}{2\f{m}{2kT}}\\
&=&N\sqrt{\f{m}{2πkT}} \\
ここで、\bar{c}&=&\s{\f{8kT}{πm}}^{\f12} より\\
Z_w&=&N･\f{\bar{c}}{4} \\
\f14\bar{c}N&=&\\
\end{eqnarray}
(4)
\begin{eqnarray}
Z_w&=&\f{4.48×10^4×2.38×10^6}{4} \\
&&(\because \bar{c}=4.48×10^2{[\rm ms^{-1}]}=4.48×10^4[{\rm cm \ s^{-1}}]) \\
&=&2.66×10^{10} \\
\end{eqnarray}
(5)
$N’$個のゲルマニウム表面積は$\f{N’}{1.3×10^{15}}[{\rm cm^2}]$であり、初期の表面ゲルマニウムの半分を酸化させるに必要な酸素分子数は$\f{N’}{2}$かつ、$\f{N’}{1.3×10^{15}}[{\rm cm^2}]$の表面積に対して1秒間に衝突する酸素分子数は$\f{N’}{1.3×10^{15}}Z_w$である。よって、求める時間$T$は
\begin{eqnarray}
T&=&\f{\f{N’}{2}}{\f{N’}{1.3×10^{15}}Z_w} \\
&=& \f{1.3×10^{15}}{2Z_w}\\
&=& \f{1.3×10^{15}}{2×2.66×10^{10}}\\
&=& 2.44×10^4[{\rm s}]\\
\end{eqnarray}