H28の問題はこちら
解答
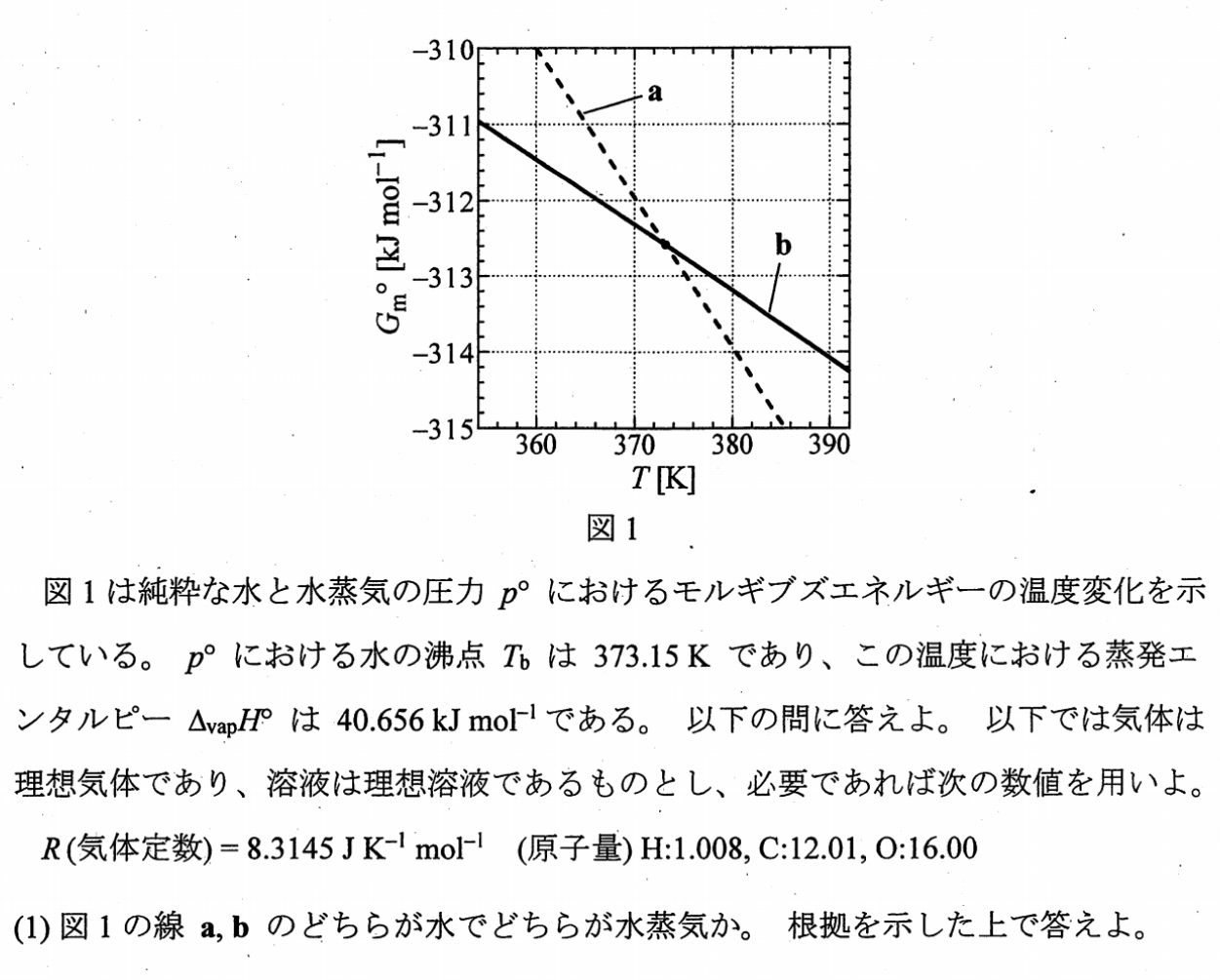
Ⅰ-(1)
グラフの交点において、$Δ_{\rm vap}G=0[{\rm kJ \ mol^{-1}}],Δ_{\rm vap}H\maru=40.656[{\rm kJ \ mol^{-1}}]$となるので、グラフの交点において、
$$\b
Δ_{\rm vap}G_m&=&Δ_{\rm vap}H\maru-TΔ_{\rm vap}S_m \\
Δ_{\rm vap}S_m&=&\f{Δ_{\rm vap}H\maru-Δ_{\rm vap}G_m}{T} \\
&=& \f{40.656}{372}>0\\
\e $$であり、エントロピーは必ず正の値をとるから、水蒸気のエントロピーの方が水のエントロピーよりも大きい。
ところで、定圧下なので、$\d G_m=-S_m\d T⇔\f{\d G_m}{\d T}=-S_m$となる。
よって、水蒸気の方がエントロピーが大きいため、直線の傾きが大きいaが水蒸気で、傾きが小さいbが水となる。
$$\b
２つの直線の傾きの差&=&\f{d G_{ma}}{\d T}-\f{\d G_{mb}}{\d T} \\
&=& \f{-S_{ma}\d T}{\d T}-\f{-S_{mβ}\d T}{\d T}\\
&=& -S_{ma}+S_{mb}\\
&=&Δ_{\rm vap }S\maru_{m} \tag{1}\\
&&このとき、等温定圧条件において、 \\
ΔG&=&ΔH-TΔS\\
ΔS&=&\f{ΔH-ΔG}{T}\\
&&となるので、(1)は\\
&=&-\f{Δ_{\rm vap}H_m\maru-Δ_{\rm vap}G_m\maru}{T}\\
\e $$となる。
クラウジウスークラペイロンの式より、
$$\b
\ln 0.900p\maru-\ln p\maru&=&-\f{Δ_{\rm vap}H\maru}{R}\s{\f{1}{T}-\f{1}{373.15}} \\
\s{\f{1}{T}-\f{1}{373.15}} &=&-\f{\ln 0.900×R}{Δ_{\rm vap}H\maru} \\
\f{1}{T}&=&-\f{\ln 0.900×R}{Δ_{\rm vap}H\maru}+\f{1}{373.15} \\
T&=&1÷\s{-\f{\ln 0.900×R}{Δ_{\rm vap}H\maru}+\f{1}{373.15}} \\
&=& 1÷\s{-\f{\ln 0.900×8.3145}{40656}+\f{1}{373.15}} \\
&=&370.17[{\rm K}] \\
\e $$となる。よって、沸点は370.17K
グルコースのモル分率$χ$は
$$\b
χ&=&\f{\f{5}{180}}{\f{95}{18}+\f{5}{180}} \\
&=& 5.23×10^{-3}\\
\e $$であるので、モル沸点上昇と溶質のモル分率との関係式より、
$$\b
ΔT&=&\s{\f{RT_{純水}^2}{Δ_{\rm vap}H\maru}}χ \\
&=& \s{\f{8.3145×373.15^2}{40656}}×5.23×10^{-3}\\
&=& 0.149[{\rm K}]\\
\e $$となる。
このグルコースのモル濃度$C$は溶液の密度が$\rm 1.00kg \ dm^{-3}$なので、
$$\b
C&=&\f{0.001×1000}{180}\\
&=&5.56×10^{-3}[{\rm mol \ dm^{-3}}] \\
&=&5.56[{\rm mol \ m^{-3}}] \\
\e $$よって、溶質のモル濃度$C$と浸透圧$Π$の関係式より
$$\b
Π&=&CRT \\
&=& 5.56×8.3145×298\\
&=&1.38×10^{4}[{\rm Pa}] \\
\e $$となる。