\begin{eqnarray}
等温過程なので&、& \\
ΔU&=&0 \\
また&、& \\
ΔU&=&TΔS-PΔV=0 なので\\
ΔS&=&\f{PΔV}{T} \\
&=& \f{PV_1}{T} \\
となる&。&また、等温定圧過程なので \\
ΔH&=& ΔU+PΔV \\
&=&0+PV_1 \\
&=&PV_1 \\
となる&。& \\
\end{eqnarray}
オットーサイクルとかルノーサイクルのp-V図は以下のようになる。
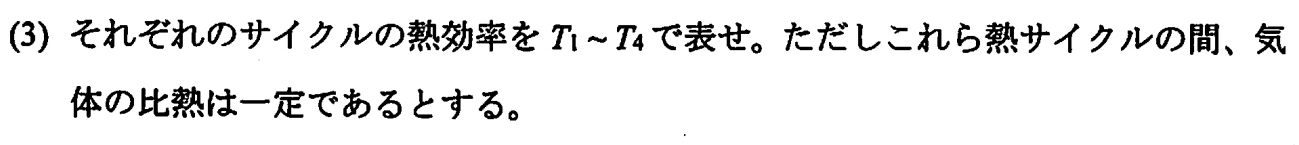まず、オットーサイクルの熱効率を求める。
各過程について内部エネルギー変化$ΔU$、もらった熱量$Q$、サイクルが外界からされた仕事$W$を求める。
①１→２
断熱過程であるから
$$\b
Q_1&=&0 \\
ΔU_1&=&W_1=C_V(T_2-T_1) \\
\e$$
②２→３
定容変化であるから
$$\b
W_2&=&0 \\
ΔU_2&=&Q_2=C_V(T_3-T_2) \\
\e$$
③３→４
断熱過程であるから
$$\b
Q_3&=&0 \\
ΔU_3&=&W_3=C_V(T_4-T_3) \\
\e$$
④４→１
定容過程であるから
$$\b
W_4&=&0 \\
ΔU_4&=&Q_4=C_V(T_1-T_4) \\
\e$$
熱効率の効率は、高熱源からもらった熱量に対する１周してサイクルが外界に対してした仕事$-W_{\rm cycle}$の比で与えられるので、
したがって、この場合は
$$\b
η&=&\f{-W_{\rm cycle}}{Q_2} \\
&=&\f{-W_1-W_2-W_3-W_4}{Q_2} \\
&=&\f{-C_V(T_2-T_1)- 0-C_V(T_4-T_3)-0 }{C_V(T_3-T_2)}\\
&=&\f{T_3-T_2+T_1-T_4}{T_3-T_2}\\
&=& 1+\f{T_1-T_4}{T_3-T_2}\\
\e$$
次にカルノーサイクルの熱効率を求める。
各過程について内部エネルギー変化$ΔU$、もらった熱量$Q$、サイクルが外界からされた仕事$W$を求める。
①１→２
断熱過程であるから
$$\b
Q_1&=&0 \\
ΔU_1&=&W_1=C_V(T_2-T_1) \\
\e$$
②２→３
定温変化であるから
$$\b
ΔU_2&=&0 \\
-W_1&=&Q_2=RT_2\ln\f{V_3}{V_2} \\
\e$$
③３→４
断熱過程であるから
$$\b
Q_3&=&0 \\
ΔU_3&=&W_3=C_V(T_4-T_3) \\
\e$$
④４→１
定温過程であるから
$$\b
ΔU_4&=&0 \\
-W_4&=&Q_4=RT_1\ln\f{V_1}{V_4} \\
\e $$
また、ここで、断熱可逆過程におけるポアソンの式$TV^{γ-1}=一定$より、
$$T_1V_1^{γ-1}=T_2V_2^{γ-1}\\
T_4V_4^{γ-1}=T_3V_3^{γ-1}$$ が成り立つ。
よって、$T_1=T_4,T_2=T_3$なので、それぞれ、左辺同士、右辺同士で割り算すると、
\begin{eqnarray}
\fp{V_1}{V_4}^{γ-1}&=&\fp{V_2}{V_3}^{γ-1}\\
\f{V_1}{V_4}&=&\f{V_2}{V_3}（\because 体積は正、γ=\f{C_P}{C_V}>1）\\
\f{V_3}{V_2}&=&\f{V_4}{V_1}\tag{1}
\end{eqnarray}
が成り立つ。
熱効率の効率は、高熱源からもらった熱量に対する１周してサイクルが外界に対してした仕事$-W_{\rm cycle}$の比で与えられるので、
したがって、この場合は
$$\b
η&=&\f{-W_{\rm cycle}}{Q_2} \\
&=&\f{-W_1-W_2-W_3-W_4}{Q_2}\\
&=& \f{-C_V(T_2-T_1)+RT_2\ln\f{V_3}{V_2}-C_V(T_4-T_3)+RT_1\ln\f{V_1}{V_4} }{RT_2\ln\f{V_3}{V_2}}\\
&=& \f{RT_2\ln\f{V_3}{V_2}+RT_1\ln\f{V_1}{V_4} }{RT_2\ln\f{V_3}{V_2}}(\because T_1=T_4,T_2=T_3)\\
&=&\f{RT_2\ln\f{V_3}{V_2}-RT_1 \ln\f{V_4}{V_1}}{RT_2\ln\f{V_3}{V_2}}\\
&=&\f{RT_2\ln\f{V_3}{V_2}-RT_1 \ln\f{V_3}{V_2}}{RT_2\ln\f{V_3}{V_2}}(\because(1))\\
&=&\f{R(T_2-T_1)\ln\f{V_3}{V_2}}{RT_2\ln\f{V_3}{V_2}}\\
&=&\f{T_2-T_1}{T_2}\\
&=&1-\f{T_1}{T_2}
\e $$
この問題の解説
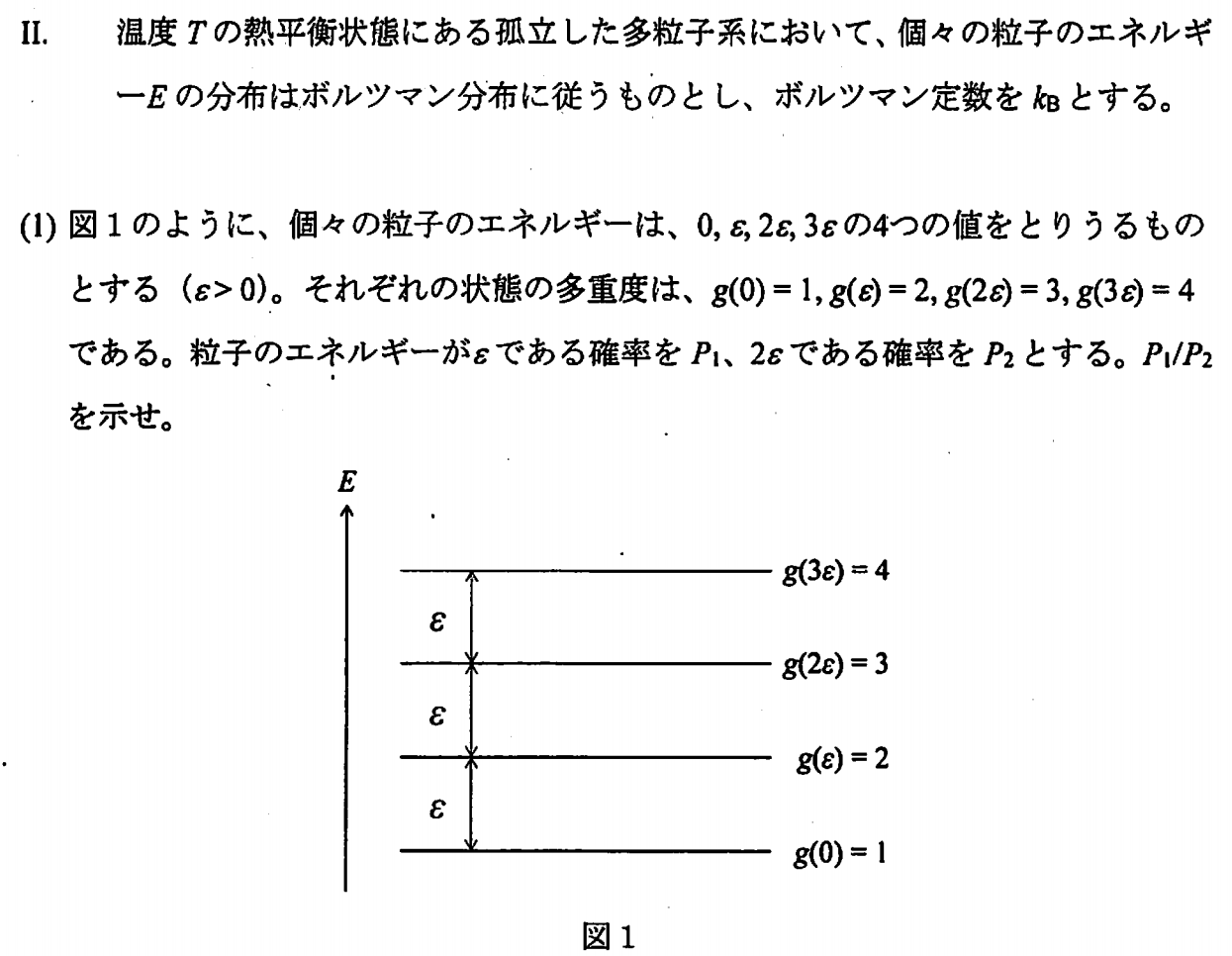
Ⅱ(1)
\begin{eqnarray}
P_l&=&\f{n_l}{N} \\
&=& \f{g(lq)exp\s{-\f{lq}{k_BT}}}{Q}\\
但し、Q&=&\sum_ig(iq)exp\s{-\f{iε}{k_BT}} \\
より、\f{P_1}{P_2}&=&\f{2\exp\s{-\f{ε}{k_BT}}}{3\exp\s{-f{2ε}{k_BT}}} \\
&=& \f{2}{3\exp\s{-f{ε}{k_BT}}}\\
\end{eqnarray}
(2)
簡単のため、$\f{1}{k_BT}=β$と置くと、問題文から
\begin{eqnarray}
U&=&-\f{\d \log Z}{\d β}=\f{1}{Z}\f{\d Z}{\d β} \\
ここで、Z&=&C\m{\sum_ig(q_i)\exp\s{-βε_i}}^N\m{Cは定数}と書けるので、 \\
U&=&\f{1}{C\m{\sum_ig(q_i)\exp\s{-βε_i}}^N}C\m{\sum_ig(q_i)\exp\s{-βε_i}}^{N-1}\sum_ig(ε_i)\exp\s{-βε_i} \\
&=& -\f{\sum_ig(q_i)(-q_i)\exp\s{-βε_i}}{\sum_i g(q_i)\exp(-βε_i)}\\
&=& \f{\sum_i ε_i \exp(-βε_i)}{\sum_i\exp(-βε_i)}\\
\end{eqnarray}
また、
\begin{eqnarray}
\sum_i \exp(-βε_i)&=&1+\exp(-βε)+\exp(-2βε)+・・・ \\
&=&1+\exp(-βε)+\m{exp(-βε)}^2+・・・ \\
&=& \f{1}{1-\exp(-βε)}(\because エネルギー準位が無限に存在する。)\\
\sum_iε_i\exp(-βε_i)&=&0.1+ε\exp(-βε)+2ε\m{\exp(-βε)}^2+・・・ =Sとおくと、\\
S-S・\exp(-βε)&=&ε\exp(-βε)+ε\m{\exp(-βε)}^2ε\m{\exp(-βε)}^3+・・・\\
ε\m{1-\exp(-βε)}&=&ε\exp(-βε)\sum_i\exp(-βε_i)\\
したがって&、&\\
S&=&\f{ε\exp(-βε)}{\m{1-\exp(-βε)}^2}\\
U&=&\f{\sum_iε_i\exp(-βε)}{\sum_i\exp(-βε_i)} \\
&=&\f{ε\exp(-βε)}{1-\exp(-βε)}\\
&=& \f{ε\exp\s{-\f{ε}{k_BT}}}{1-\exp\s{-\f{ε}{k_BT}}} \\
\end{eqnarray}