(+)と(-)について
旋光計で有機分子溶液を観測したとき、
右回り(時計回り)の旋光性を持つ有機分子は(+)-(分子名)と表す。
左回り(反時計回り)の旋光性を持つ有機分子は(-)-(分子名)を表す。
比旋光度とは
旋光計で得られた観点角α は光が出会う光学活性な分子数に比例する。
そのため濃度を2倍すると回転角は2倍になるし、
旋光計の試料管の長さを2倍にしても回転角は2倍になる。
つまり、旋光角α は試料の濃度と試料管の長さに影響される。
そのため、単位長さと単位濃度当たりの旋光度というものが存在している。
それが比旋光度というものだ。このときの単位長さは[dm]で、単位濃度は[g/cm3]である。
$$[\a]=\f{観測した回転角[°]}{試料管の長さ[dm]×試料濃度[g・cm^-3]}$$
エナンチオマー過剰率
例題)
化石中の(+)―アラニンは[α]=+4.25の比旋光度を示した。
純粋な(+)―アラニンの比旋光度を[α]=+8.5とするとき、
このときのエナンチオマー過剰率を求めよ。
これを解くのは非常に簡単だ。
\begin{align}&エナンチオマー過剰率(\%)\\&=主エナンチオマーの割合(\%)-副エナンチオマーの割合(\%)\\&=打ち消されなかった主エナンチオマーの割合(\%)\\&=\f{混合物の比旋光度}{主エナンチオマーが仮に純粋だったときの比旋光度}\\&=\f{+4.25}{+8.5}×100\\&=50[\%]\end{align}
さて、問題を解くこと自体は混合物の比旋光度をその混合物の主エナンチオマーについての純粋な比旋光度で割れば出てくる。
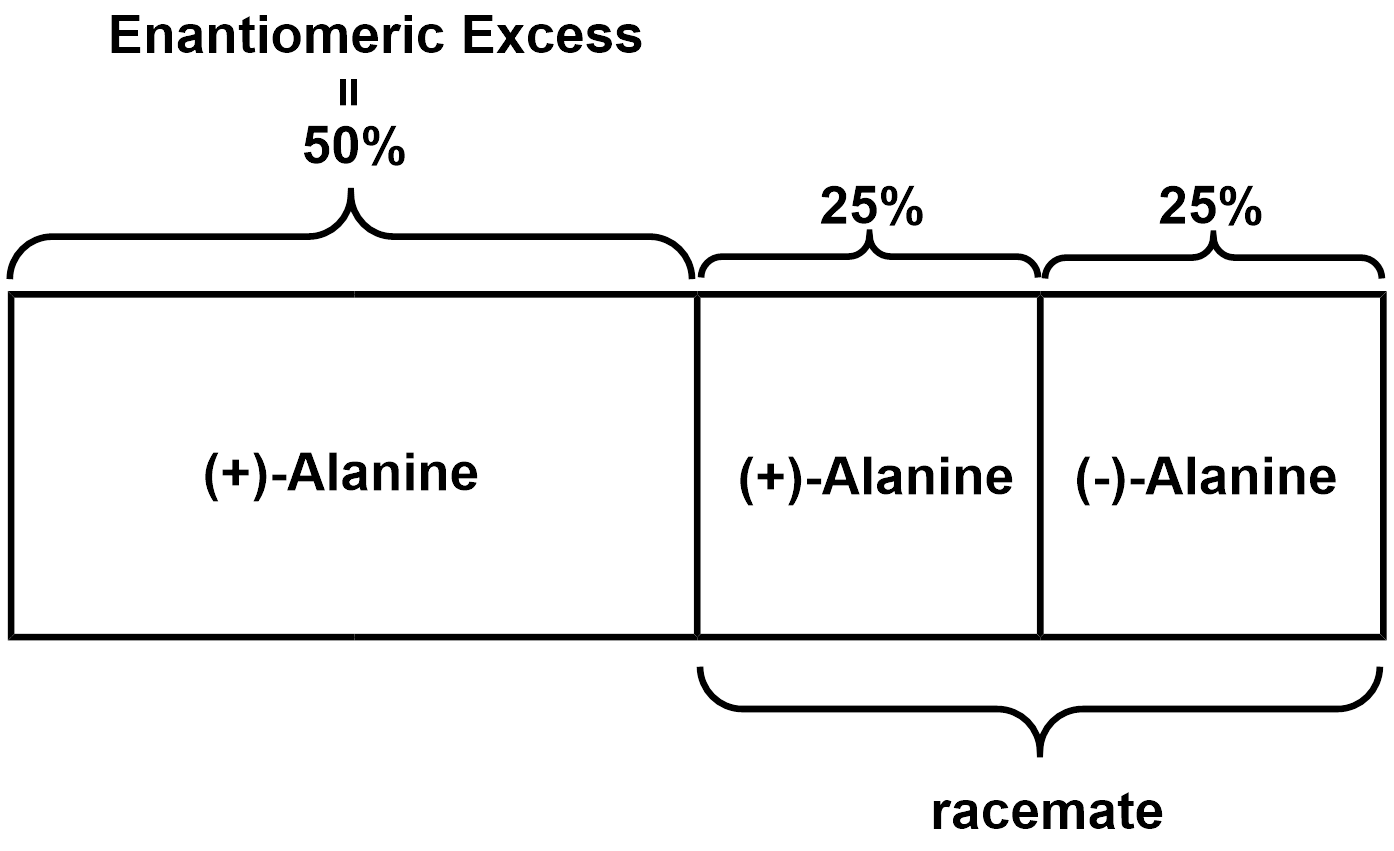
これを感覚的に理解するために図も掲載しておく。
この問題を図にすると以下のような感じだ。
(eeはエナンチオマー過剰率(Enantiomeric Excess)の略称)
これを見れば、
\begin{align}&エナンチオマー過剰率(\%)\\&=主エナンチオマーの割合(\%)-副エナンチオマーの割合(\%)\\&=打ち消されなかった主エナンチオマーの割合(\%)\end{align}
の意味が分かるだろう。
参考
ボルハルト・ショアー現代有機化学 上 第6版 p.218