フローチャートを書いてみました。
以下は簡単な補足です。
$C_{\rm n}$…$\f{360°}{n}$回転回したときに一致する軸のことです。
$σ$面…対称面のことです。2種類あります。$σ_{\rm v}$と$σ_{\rm h}$です。
主軸に対して平行な軸を$σ_{\rm v}$、主軸に対して垂直な軸を$σ_{\rm h}$といいいます。
※主軸…一番nの大きい回転軸$C_{\rm n}$のこと。
対称中心があるか？ないか？…原点対称かどうか？
回映軸…アレンなどは180°回転させても鏡像関係になり、重ならない軸があります。これを回映軸といいます。$S_{\rm n}=σ_{\rm h}×C_{\rm n}$の関係にあります。ただ、$S_{\rm n}$がある場合は必ず$C_{\rm n}$も存在します。
以下が点群の決め方の練習問題です。
(1)
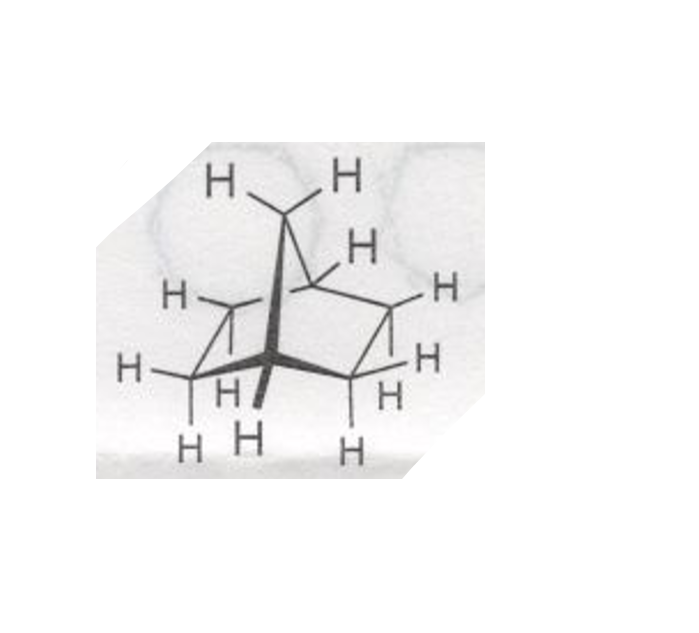答え
$C_{\rm 2v}$
線形ではない→特別に高い対称ではない→$C_{\rm n}$がある→回映軸のみではない→$C_{\rm 2}$の１つを主軸とする→主軸$C_{\rm 2}$軸に直交する2本の$C_{\rm 2}$軸はない→$σ_{\rm h}$面はない→$2枚のσ_{\rm v}$はある→$C_{\rm 2v}$
(2)
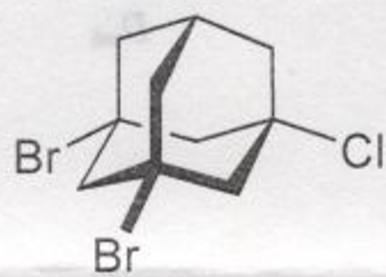
答え
$C_{\rm s}(≡S_1)$
線形ではない→特別に高い対称ではない→$σ$面はある→$C_{\rm s}(≡S_{1})$
(3)
答え
$C_{\rm s}(≡S_1)$
線形ではない→特別に高い対称ではない→$C_{\rm n}$軸はない→$σ$面はある→$C_{\rm s}(≡S_1)$
(4)
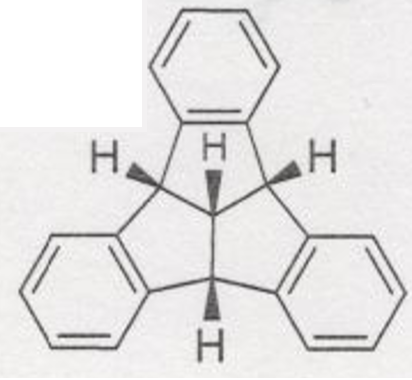
答え
$C_{\rm 3v}$
線形ではない→特別に高い対称ではない→$C_{\rm n}$がある→回映軸のみではない→$C_{\rm 3}$の１つを主軸とする→主軸$C_{\rm 3}$軸に直交する$C_{\rm 2}$軸はない→$σ_{\rm h}$面はない→3枚の$σ_{\rm v}$はある→$C_{\rm 3v}$
(5)
答え
$D_{\rm 2d}$
線形ではない→特別に高い対称ではない→主軸は直交する$C_{\rm 2}$軸が2本ある→$σ_{\rm h}$面はある→$σ_{\rm h}$面はない→$D_{\rm 2d}$
(6)
答え
$D_{\rm 2h}$
線形ではない→特別に高い対称ではない→$C_{\rm n}$がある→回映軸のみではない→$C_{\rm 2}$の１つを主軸とする→主軸$C_{\rm 2}$に直交する2本の$C_{\rm 2}$軸はある→2枚の$σ_{\rm v}$面はある→さらに$σ_{\rm h}$もある→$D_{\rm 2h}$
(7)
答え
$C_{\rm 2}$
線形ではない→特別に高い対称ではない→$C_{\rm n}$がある→回映軸のみではない→$C_{\rm 2}$の１つを主軸とする→主軸$C_{\rm 2}$軸に直交する2本の$C_{\rm 2}$軸はない→$σ_{\rm h}$面はない→$σ_{\rm v}$もない→$C_{\rm 2}$
(8)
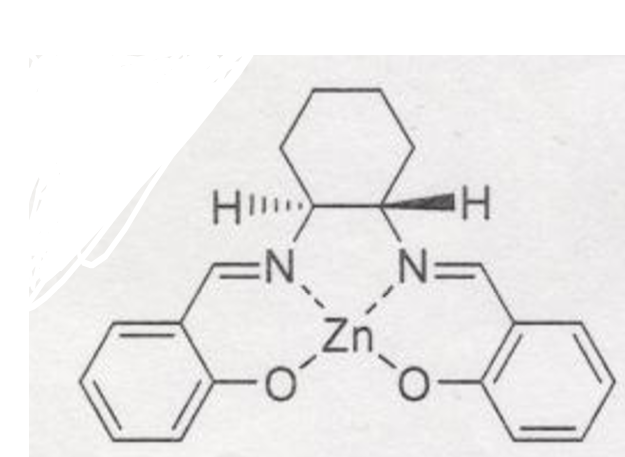
答え
$C_{\rm 2}$
線形ではない→特別に高い対称ではない→$C_{\rm n}$がある→回映軸のみではない→$C_{\rm 2}$の１つを主軸とする→主軸$C_{\rm 2}$軸に直交する2本の$C_{\rm 2}$軸はない→$σ_{\rm h}$面はない→$σ_{\rm v}$もない→$C_{\rm 2}$