理想気体の状態方程式より、
$$\b pV_m^{\maru}&=&RT\\
\f{pV_m}{RT}&=&1\\
Z&=&1
\e$$より、(ア)に当てはまる数字は 1 です。
実在気体において、
$$Z=\f{pV_m}{RT}\tag1$$が成り立ちます。理想気体においては、
$$\b Z&=&\f{pV_m^{\maru}}{RT}\\
1&=&\f{pV_m^{\maru}}{RT}(\because 理想気体においてZ=1)\\
\f{p}{RT}&=&\f{1}{V_m^{\maru}}\tag2
\e$$が成り立ちます。よって、$(2)$式を$(1)$式に代入すると、
$$Z=\f{V_m}{V_m^{\maru}}$$が得られます。
一般的に、分子サイズより短い領域の支配的な相互作用は斥力的であり、
分子サイズより長い領域の支配的な相互作用は引力的です。
実在気体のメタンは、理想気体と違い、分子間相互作用や分子自体の体積がある。低圧領域では分子自体の体積は全体の体積とくらべて無視できる大きさであるため、分子間相互作用が支配的になり、$V_m<V_m^{\maru}$となる。つまり、$Z<1$となる。一方、高圧領域になればなるほど、分子の体積による影響が支配的になり、$V_m>V_m^{\maru}$となる。つまり$Z>1$となる。
(153文字)
$$pV_m=RT(1+B’p+C’p^2+・・・)$$ において、$p→0$の極限ではは$p^n(n>0)$は二次近似以上になるので、無視できます。(つまり第3ビリアル係数以降の影響は無視できる)。
よって、$p→0$において
$$\b pV_m&=&RT(1+B’p)\\
Z&=&1+B’p\\
\df{Z}{p}&=&B'(圧力pで両辺を微分)
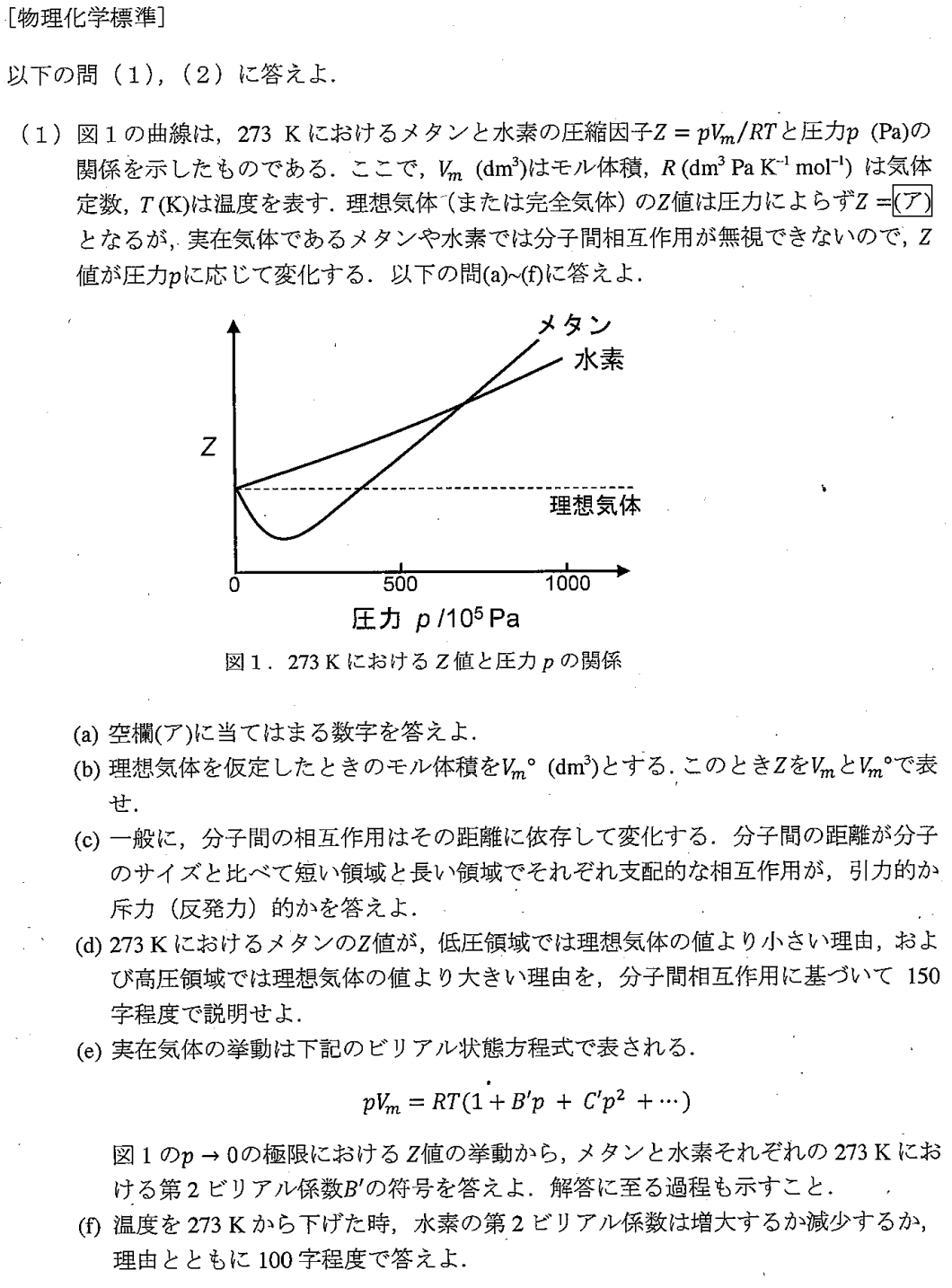
\e$$ が成り立ちます。つまり、第2ビリアル係数は$Z-p$グラフの$p→0$の極限における傾きです。そこで、グラフより、
水素の第2ビリアル係数は正、(p→0付近において傾きが正)
メタンの第2ビリアル係数は負(p→0付近において傾きが負)
となります。
低温になるほど気体の分子運動エネルギーが小さくなり、温度に依存しない分子間相互作用の影響が相対的に増加する。そのため、モル体積は(つまりZの大きさ)は減少する。よって第2ビリアル係数は減少すると考えられる。(103文字)

$\newcommand\nn{[{\rm N_2O_5}]}
\newcommand\noo{[{\rm NO_2}]}
\newcommand\no{[{\rm NO}]}
\newcommand\nooo{[{\rm NO_3}]}
\newcommand\ka{k_{\rm a}}
\newcommand\kaa{k_{\rm a’}}
\newcommand\kb{k_{\rm b}}
\newcommand\kc{k_{\rm c}}
$
$$\b
\df{\no}{t}&=&\kb\noo\nooo-\kc\no\nn\\
\df{\nooo}{t}&=&\ka\nn-\kaa\noo\nooo-\kb\noo\nooo\\
\e$$
(2)-(h)の解説
$$\df{\nn}{t}=-\ka\nn+\kaa\noo\nooo-\kc\no\nn\tag{☆}$$ 定常状態近似より、
$$\b
\df{\no}{t}&=&\kb\noo\nooo-\kc\no\nn=0\tag1\\
\df{\nooo}{t}&=&\ka\nn-\kaa\noo\nooo-\kb\noo\nooo=0\tag2\\
\e$$ $(1)$式より
$$\no\nn=\f{\kb}{\kc}\noo\nooo\tag3 $$$(3)$式を$(☆)$式に代入
$$\df{\nn}{t}=-\ka\nn+\kaa\noo\nooo-\kb\noo\nooo\tag{★} $$$(2)$式より
$$\noo\nooo=\f{\ka}{\kaa+\kb}\nn\tag4$$ $(4)$式を$(★)$式に代入すると、
$$\df{\nn}{t}=\left(-\ka+\f{\ka\kaa}{\kaa+\kb}-\f{\ka\kb}{\kaa+\kb}\right)\nn $$よって、$\left(-\ka+\f{\ka\kaa}{\kaa+\kb}-\f{\ka\kb}{\kaa+\kb}\right)=-K$と置くと、
$$\df{\nn}{t}=-K\nn$$となり、題意は示された。
(2)-(i)の解説
$$\b
\df{\nn}{t}&=&-K\nn\\
\f{\d\nn}{\nn}&=&-K\d t\\
\ln{\nn}&=&-Kt+C(Cは積分定数)\\
\e$$ $\nn$の初期濃度を$\nn_0$とすると
$$\ln{\nn_0}=C(t=0を代入)$$ よって、
$$\b \ln{\nn}&=&-Kt+\ln{\nn_0}\\
\ln{\f{\nn}{\nn_0}}&=&-Kt\\
-\ln{\f{\nn}{\nn_0}}&=&Kt
\e$$ よって、$\nn$の分解過程が一次であることを示すためには縦軸を$-\ln{\f{\nn}{\nn_0}}$,横軸を$t$にとったグラフが1次関数、つまり、直線に成ることを示せば良い。実際、
となるので、確かにそうなる。
(0.35は与えられているので計算できますが、0.70と1.1は計算せずに、0.35を2倍、3倍した数字を書いています。実際パソコンで計算すると、0.71、1.08(つまり0.71と1.1)となります。手計算することは不可能なので実際はこのような解答にならざるをえないと思います。)
また、速度定数$K$はこのグラフの傾きなので、
$$K=\f{0.35}{200}=1.75×10^{-3}≒1.8×10^{-3}[{\rm s^{-1}}]$$ となる。