(a)
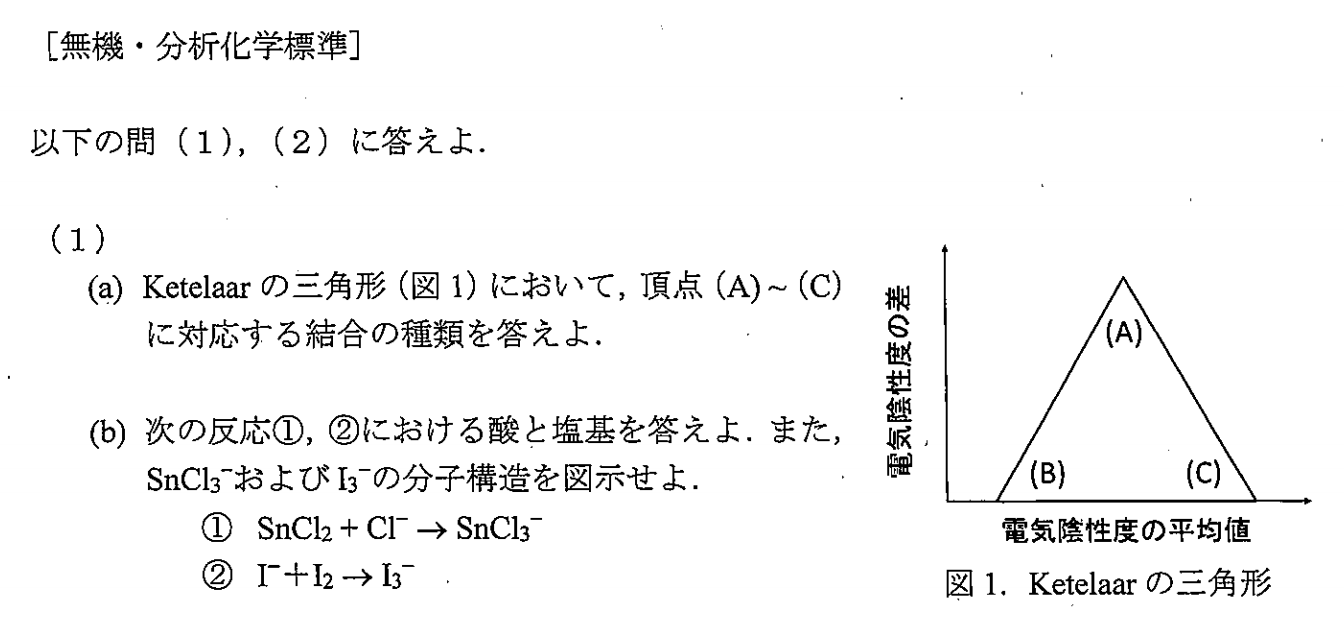
(A)イオン結合
(B)金属結合
(C)共有結合
(b)
①
酸：$\rm SnCl_2$
塩基：$\rm Cl^-$
②
酸：$\rm I^-$
塩基：$\rm I_2$
錯体の生成定数を$β$とすると、$\log β$はギブズの自由エネルギー$ΔG$に比例する。そして、この$ΔG$は$ΔG=ΔH-TΔS$と表され、多座配位子のほうが、ΔSが大きくなるので、他座配位子のほうが$ΔG$が小さくなる。よって、多他座配位子錯体の生成定数のほうが大きくなる。
スピネルの単位格子において、金属が入る間隙は、四面体間隙：八面体間隙＝1:2の割合で存在する。四面体間隙に二価の金属イオン、八面体間隙に三価の金属イオンが入るのが正スピネルで、四面体間隙に三価の金属イオンがはいり、残りが八面体間隙に入るのが逆スピネルである。よって、
それぞれの配位子場安定化エネルギーは以下のようになる。
正スピネル
四面体間隙$\rm Cu^{2+}$・・・$\f25Δ_t$
八面体間隙$\rm Fe^{3+}$・・・$0$
逆スピネル
四面体間隙$\rm Fe^{3+}$・・・$0$
八面体間隙$\rm Fe^{3+}$・・・$0$
八面体間隙$\rm Cu^{2+}$・・・$\f35Δ_o$
よって、以上より、逆スピネルのほうが配位子場安定化エネルギーが大きいので、$\rm CuFe_2O_4$は逆スピネル構造をとると予想できる。
$E\stst$=1.765[{\rm V}]$
