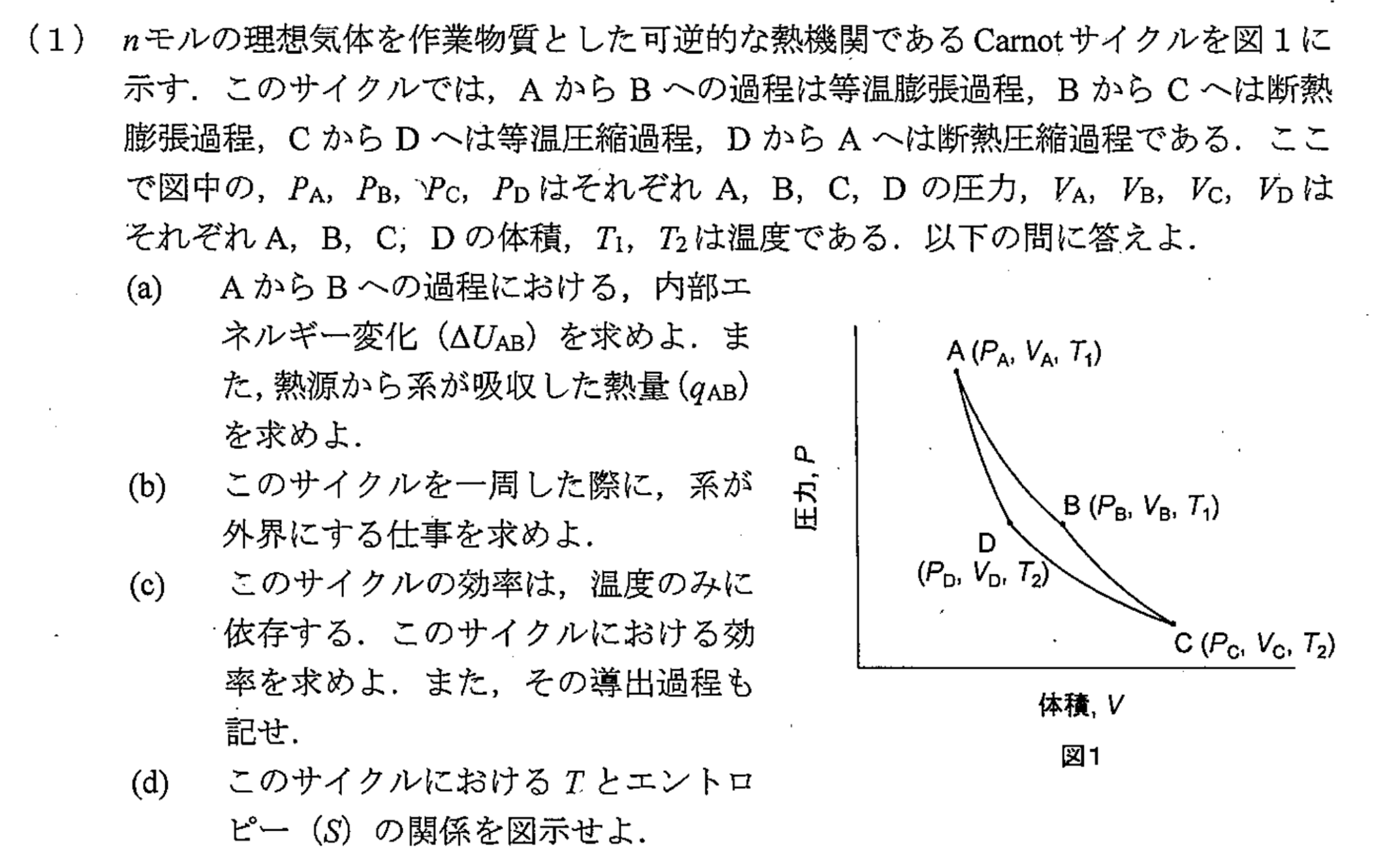
Carnatサイクルにおいて、すべての過程は可逆過程です。(正確には準静的過程)
なので、以下、等温膨張過程→等温可逆膨張などと言い換えます。(製作者中の語彙の統一性に重きにおきました。)ご注意ください。
理想気体において、内部エネルギーは温度のみの関数であるので、温度変化しない等温可逆膨張において、内部エネルギー変化$ΔU_{AB}$は
$$ΔU_{AB}=0$$となります。さらに、熱力学第一法則より
\begin{eqnarray}
ΔU_{AB}&=&q_{AB}+W_{AB}=0\\
q_{AB}&=&-W_{AB}\tag1
\end{eqnarray}
となる。
ところで、$A→B$の等温可逆過程におけるすべての地点で以下の式が成り立ちます。
$$P_{系}=\f{nRT_{1}}{V_{系}}$$カルノーサイクルの等温可逆過程においては、準静的過程を仮定しているので、以下が成り立ちます。
$$P_{系}=P_{外界} $$また、$A→B$までに系が外界にした仕事の微小表現は以下のようになります。
$$-δW=P_{外界}{\rm d}V_{系}=P_{系}{\rm d}V_{系}\tag2 $$よって、$A→B$までに系が外界にした仕事$-W_{AB}$は以下のようになります。
\begin{eqnarray}
-W_{AB}&=&\it_{A}^{B}-δW_{AB}\\
&=&\it_{V_A}^{V_B}P_{系}{\rm d}V_{系}(\because (2)式を代入)\\
&=&\it_{V_A}^{V_B}\f{nRT_{1}}{V_{系}}{\rm d}V_{系}(\because (1)式を代入)\\
&=&nRT_{1}\it_{V_A}^{V_B}\f{1}{V_{系}}{\rm d}V_{系}\\
&=&nRT_{1}\ln{\f{V_A}{V_B}}
\end{eqnarray}
よって、$(1)$式より、
$$q_{AB}=-W_{AB}=nRT_{1}\ln{\f{V_A}{V_B}}$$となります。
詳しくは等温可逆過程を参照ください。
まず、$B→C$の断熱可逆膨張について考えます。
この温度変化範囲では熱容量$C_V=一定$であると仮定します。
また、理想気体の場合、分子間に相互作用がなく、気体分子同士を引き離すのにエネルギーが必要ないため、すなわち体積を膨張させても内部エネルギーは変わりません。そのため、理想気体に限り、体積が変わっても$dU=C_V{\rm d}T$が成り立ちます。よって、
\begin{eqnarray}
\it^{U_C}_{U_B}{\rm d}U &=&\it^{T_2}_{T_1}C_V{\rm d}T\\
ΔU_{BC}&=&C_V(T_2-T_1)\tag3
\end{eqnarray}
となります。よって、、熱力学第一法則より、
\begin{eqnarray}
ΔU_{BC}&=&q_{BC}+W_{BC}\\
ΔU_{BC}&=&W_{BC}(\because 断熱過程であるのでq_{BC}=0)\\
-W_{BC}&=&-ΔU_{BC}=-C_V(T_2-T_1)(\because (3)式を代入)
\end{eqnarray}
上記と同じような計算より、
$C→D$への等温可逆収縮において系がした仕事$-W_{CD}$と
$D→C$への断熱可逆収縮において系がした仕事$-W_{DA}$はそれぞれ
\begin{eqnarray}
-W_{CD}&=&nRT_{2}\ln{\f{V_C}{V_D}}\\
-W_{DA}&=&-C_V(T_1-T_2)
\end{eqnarray} となります。よって、このサイクルが一周したときに系が外界にする仕事$-W_{\rm cycle}$は
\begin{eqnarray}
-W_{\rm cycle}&=&-W_{AB}-W_{BC}-W_{CD}-W_{DA}\\
&=&nRT_{1}\ln{\f{V_A}{V_B}}-C_V(T_2-T_1)+nRT_{2}\ln{\f{V_C}{V_D}}-C_V(T_1-T_2)
&=&nRT_{1}\ln{\f{V_A}{V_B}}+nRT_{2}\ln{\f{V_C}{V_D}}\tag4
\end{eqnarray}
ここで、断熱可逆過程におけるポアソンの式$TV^{γ-1}$より、
$$T_1V_B^{γ-1}=T_2V_C^{γ-1}\\
T_1V_A^{γ-1}=T_2V_D^{γ-1}$$が成り立つので、この2式の両辺同士を割ると
\begin{eqnarray}
\fp{V_B}{V_A}^{γ-1}&=&\fp{V_C}{V_D}^{γ-1}\\
\fp{V_B}{V_A}&=&\fp{V_C}{V_D}\tag5
\end{eqnarray}
となります。よって、$(5)$式を$(4)$式に代入すると、
\begin{eqnarray}
-W_{\rm cycle}&=&nRT_{1}\ln{\f{V_A}{V_B}}+nRT_{2}\ln{\f{V_C}{V_D}}\\
&=&nR(T_{1}-T_2)\ln{\f{V_A}{V_B}}
\end{eqnarray}
となります。以上が(1)-(b)への解答です。詳しくはカルノーサイクルをご参照ください。
サイクルの効率$μ$は
\begin{eqnarray}
μ&=&\f{-W_{\rm cycle}}{q_{AB}}\\
&=&\f{nR(T_{1}-T_2)\ln{\f{V_A}{V_B}}}{nRT_{1}\ln{\f{V_A}{V_B}}}\\
&=&\f{T_1-T_2}{T_1}\\
&=&1-\f{T_2}{T_1}
\end{eqnarray}
となり、たしかに温度のみに依存することがわかります。詳しくはカルノーサイクルをご覧ください。
以下のようになります。

等温定圧条件下において、化学ポテンシャル$μ$は部分モルギブス自由エネルギー$G_m$と等しいです。すなわち、
$${\rm d}μ={\rm d}G_m=-S_m{\rm d}T+V_m{\rm d}P\tag1\\
(S_mは部分モルエントロピー、V_mは部分モル体積)$$ となります。この時、圧力の増減は考慮しないので$dP=0$とすると、$(1)$式より、
$$\b
\d μ&=&-S_m \d T\\
\f{\d μ}{\d T}&=&-S_m
\e$$
となります。したがって、化学ポテンシャル$μ$の温度変化は部分モルエントロピー$S_m$に依存し、かつ、$S_m≧0$なので、化学ポテンシャルは温度増加に伴い、減少します。
(3)は解答製作中