
 以上のようなボルンバーバーサイクルの図がかける。そのため、
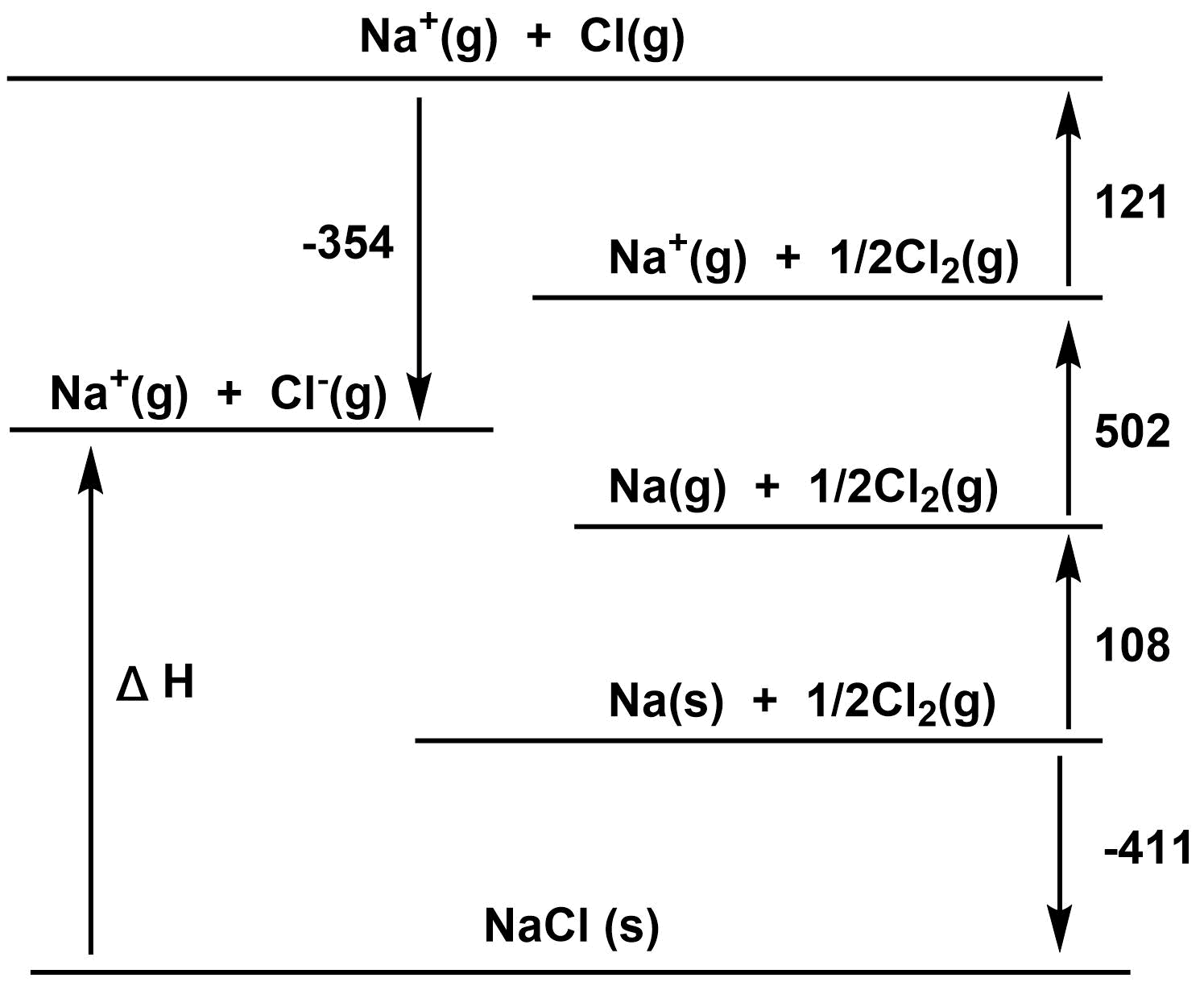
以上のようなボルンバーバーサイクルの図がかける。そのため、
$$ΔH\stst=121+502+108+411-354=788[{\rm kJ/mol}]$$
となる。

第三近接イオン以上は無視すると、
$M=1×6-\f{1}{\sqrt 2}×12=6-4\sqrt 2=6-6×1.4=-2.4$
となります。
そのため、第三近接イオン以上を無視した場合、NaCl結晶は安定に存在することができません。
※第三近接以上のイオンを無視するという条件は、NaClの単位格子に含まれるイオンだけを考えているということになります。そのため、いつも私達が見ているNaClの単位格子だけでは安定して存在することができないということになります。
マーデルング定数は正であればその結晶は安定して存在します。
NaCl結晶全体のマーデルング定数は約1.7です。

マーデルング定数が同じである場合は、イオン間距離が短いほど格子エンタルピーは大きくなる。そのため格子エンタルピーは$\rm LiF>LiCl>LiBr>LiI$となる。

金属の自由電子が結晶の中で酸素原子が$\rm O^{2-}$のイオンとして存在するために用いられるために、酸素の割合が多ければ多いほど自由電子が少なくなるため導電性が低下すると思われます。
※侵入型水素化物は導電性や常磁性が下がります。これは、水素原子がヒドリドとして金属内に存在しているためです(つまり自由電子がヒドリドの価電子としてもちいられ、自由電子数が現象する)。その推論です。間違いであればごめんなさい。
 (a)6
(a)6
(b)4
(c)3
 \begin{eqnarray}
\begin{eqnarray}
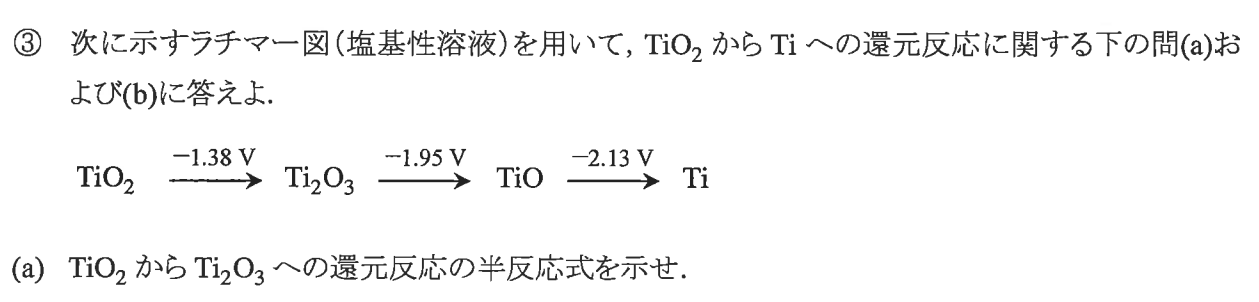
\rm TiO_2&→&\rm Ti_2O_3 \\
\rm 2TiO_2&→&\rm Ti_2O_3+H_2O \\
\rm 2TiO_2+2H^+&→&\rm Ti_2O_3+H_2O \\
\rm 2TiO_2+2H^++e^-&→&\rm Ti_2O_3+H_2O \\
\end{eqnarray}
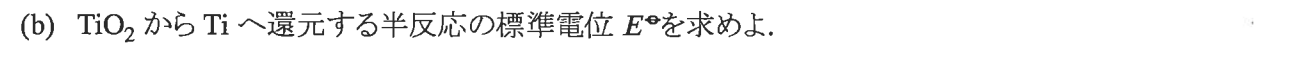 $$E\stst=\f{-1.38-1.95-2.13×2}{4}=1.8975=1.90{[\rm V]}$$
$$E\stst=\f{-1.38-1.95-2.13×2}{4}=1.8975=1.90{[\rm V]}$$
 (i)例えば、$\rm TiO_2$の価電子が紫外線により励起され、同時に正孔を生成する。この正孔は水を酸化し酸素に、励起電子は水を還元し水素にする。このような現象を本田ー藤島効果という。
(i)例えば、$\rm TiO_2$の価電子が紫外線により励起され、同時に正孔を生成する。この正孔は水を酸化し酸素に、励起電子は水を還元し水素にする。このような現象を本田ー藤島効果という。