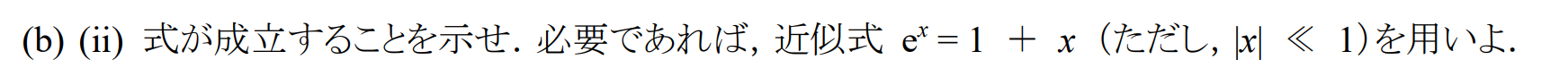\begin{eqnarray}
E&=&\f{c_2^2a_c+2c_cC_oβ+c_o^2a_o}{c_c^2+c_o^2+2c_cc_oS} \\
(c_c^2+c_o^2+2c_cc_oS)E&=&c_c^2a_o+2c_cc_oβ+c_o^2a_o\tag{※} \\
両辺を&、&C_cで偏微分して、 \\
(2c_c+2c_oS)E+(c_c^2+c_o^2+2c_oc_oS)\f{\p E}{\p c_c}&=&2c_cα_c+2c_oβ \\
\f{\p E}{\p c_2}&=& 0より\\
2(c_c+c_oS)E&=&2c_cα_c+2c_oβ \\
(α_c-E)c_c+(β-ES)c_o&=&0 \\
同様にして&、&(※)を両辺c_cで偏微分して、 \\
(β-ES)c_c+(α_0-E)c_o&=&0 \\
したがって&、& \\
{\begin{pmatrix}
α_c-E & β-ES \\
β-ES & α_o-E \\
\end{pmatrix}}
{\begin{pmatrix}
c_c \\
c_o \\
\end{pmatrix}}&=&0 \\
c_cとc_oが&、&自明な解以外を持つためには、 \\
{\begin{vmatrix}
α_c-E& β-ES\\
β-ES& α-E \\
\end{vmatrix}}&=& 0 \\
が成り立つ&。& \\
\end{eqnarray}
ヒュッケル近似では$S=0$と置くので
\begin{eqnarray}
{\begin{vmatrix}
α_c-E & β \\
β& α_o-E \\
\end{vmatrix}}&=&0 \\
(α_c-E)(α_o-E)-β^2&=&0 \\
E^2-(α_c+α_o)E+α_cα_o-β^2&=&0 \\
E&=&\f{(α_c+α_o)±\sqrt{(α_c+α_o)^2-4(α_cα_o-β^2}}{2} \\
&=&\f{α_c+α_o±\sqrt{(α_c-α_o)^2+4β^2}}{2} \\
これにα_c&=&α、α_o=α+βを代入して、 \\
E&=&\f{2α+β±\sqrt{5β^2}}{2} \\
&=& \f{2α+(1±\sqrt{5})β}{2} \\
&=& α+\s{\f{1±\sqrt{5}}{2}}β \\
したがって&、& メタナールの全π電子エネルギーはβ<0であることに注意して \\
\s{α+\f{1±\sqrt{5}}{2}β}×2&=&2α+(1+\sqrt{5})β \\
\end{eqnarray}
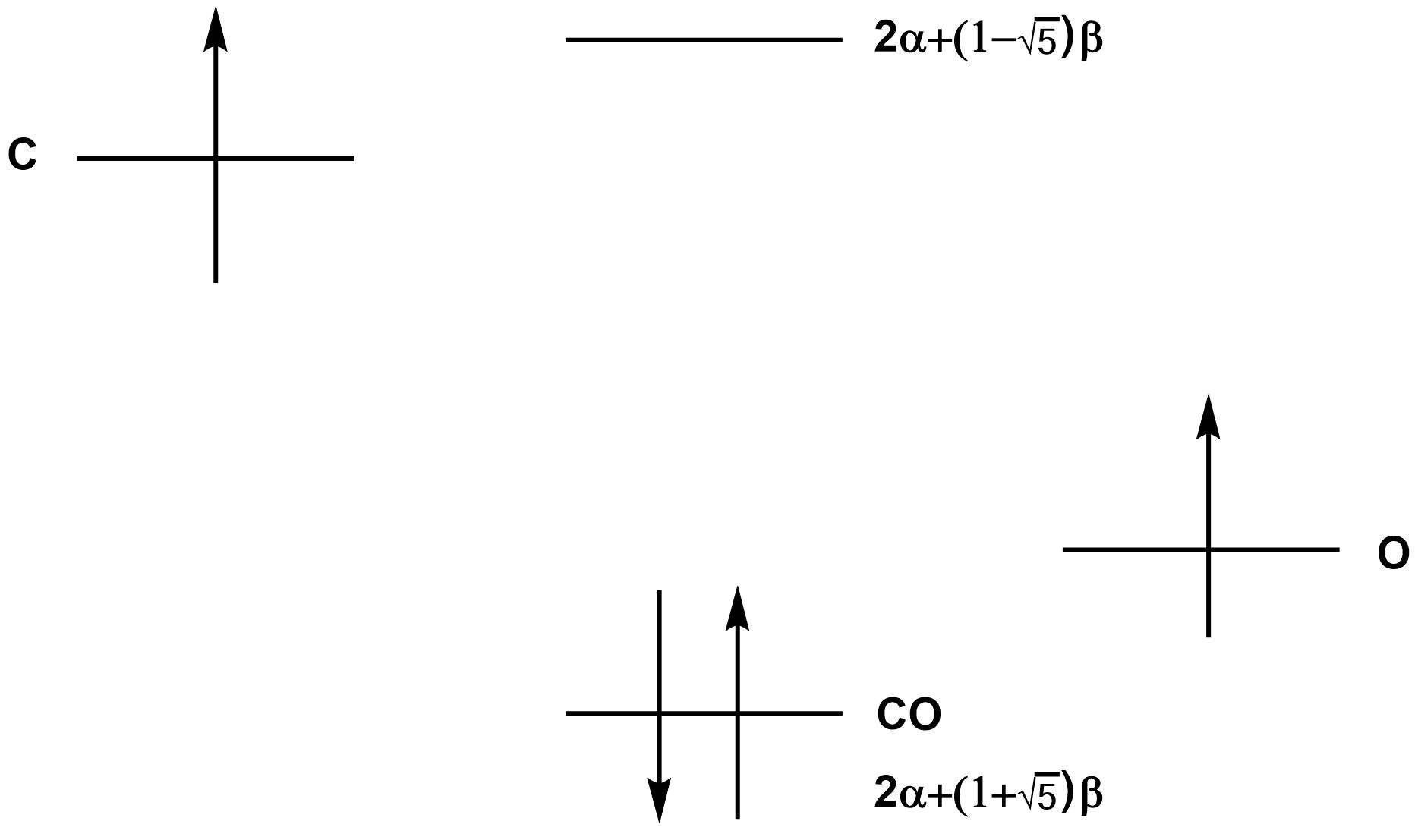炭素原子のp軌道エネルギーは$α$、酸素原子のp軌道エネルギーは$α+β$であるため、π結合を形成することで、$\sqrt{5}β$だけエネルギーが安定化する。
④
2-プロパナールの全$π$電子エネルギーは
\begin{eqnarray}
2(α+1.879β)+(α+β)&=&3α+4.758β \\
エテンの全&π&電子エネルギーは、α＋βである。 \\
したがって&、&非局在化エネルギーは \\
(3α+4.758β)-\m{(2α+2.236β)+(α+β)}&=&1.522β \\
\end{eqnarray}
(1)
①
a$\f{N_AkT}{p\stst}K^‡[A][B]$
b$κν\f{N_AkT}{p\stst}\f{kT}{hν}\f{N_A\bar{q_m}}{q_Aq_B}\exp\s{-\f{ΔE_0}{N_AkT}}=\f{N_A^2k^2T^2\bar{q}_M}{p\stst hq_Aq_B}e^{\frac{ΔE_0}{N_AkT}}$
cアイリング
②
$β=\f{1}{kT}$とすると、
\begin{eqnarray}
q&=&e^{-\f{ε}{kT}}
&=&\sum e^{β(ε_T+ε_V+ε_R)} \\
&=& \sum e^{βε_T} \sum e^{βε_v} \sum e^{βε_R}\\
&=&q_Tq_Vq_R \\
\end{eqnarray}
(a)
$q_V=\sum_v\exp\s{-\f{q_V}{kT}}$かつ、$ε_V=hν\s{v+\f12}$であるから、
$$q_V=\sum_v\exp\s{-\f{hν\s{v+\f12}}{kT}}$$
＝＝＝＝＝＝＝＝＝＝
\begin{eqnarray}
q_V&=&\sum_ie^{βε_i} \\
&=& \sum_ie^{-βhν(v_i+\frac12)}\\
&=& e^{-β\frac{hν}{2}}\sum_ie^{-βhνv_i}\\
&=& e^{-β\frac{hν}{2}}\s{1+e^{-βhν}+\s{e^{-βhν}}^2+\s{e^{-βhν}}^3+・・・}\\
&=&e^{-β\frac{hν}{2}}・\f{kT}{hν} \\
&=&
\end{eqnarray}
＝＝＝＝＝＝＝＝
(b)$v=0$の零点エネルギー$\f12hν$を基準として考えると、振動分配関数$q_V$は
\begin{eqnarray}
q_V&=&\sum_v\exp\s{-\f{hνv}{kT}}となる \\
q_V&=&\sum\exp\s{-\f{hνv}{kT}} \\
&=& 1+\exp\s{-\f{hν}{kT}}+\\
&=& \\
&=& \\
\end{eqnarray}
(2)③
$\sqrt{5}β$だけエネルギーが安定化する。
