ケテラーの三角形とは、
ある化学結合が、イオン結合、共有結合、金属結合のうち、どれにあたるのかを決めるための線引として1940年代にケテラーの手によって作られた粗い目安のことです。
ケプラーの三角形によれば、この３つの結合は、結合を形成する２つの元素の電気陰性度の差$Δχ$とその２つの元素の電気陰性度の平均$χ_{\rm mean}$(「mean」は英語で算術平均の意)によって区別することができます。
まず、イオン結合は電気陰性度の大きな差によって特徴づけられます。差が大きければ、一つの元素の電気陰性度が高く、もう一方が低いということになるので、平均の電気陰性度は中間程度の値になるはずです。
対して、共有結合は電気陰性度の差が小さいことで特徴づけられます。共有結合が支配的な二元系化合物は一般に非金属元素から作られていて、かつ、非金属元素は一般的に高い電気陰性度を持ちます。そのため、平均の電気陰性度は高い値になります。
金属結合も電気陰性度の差が小さいことで特徴づけられます。ただし、金属元素の電気陰性度は一般的に低いため、平均の電気陰性度は低くなります。
以上を踏まえて、整理されたのが以下のグラフです。
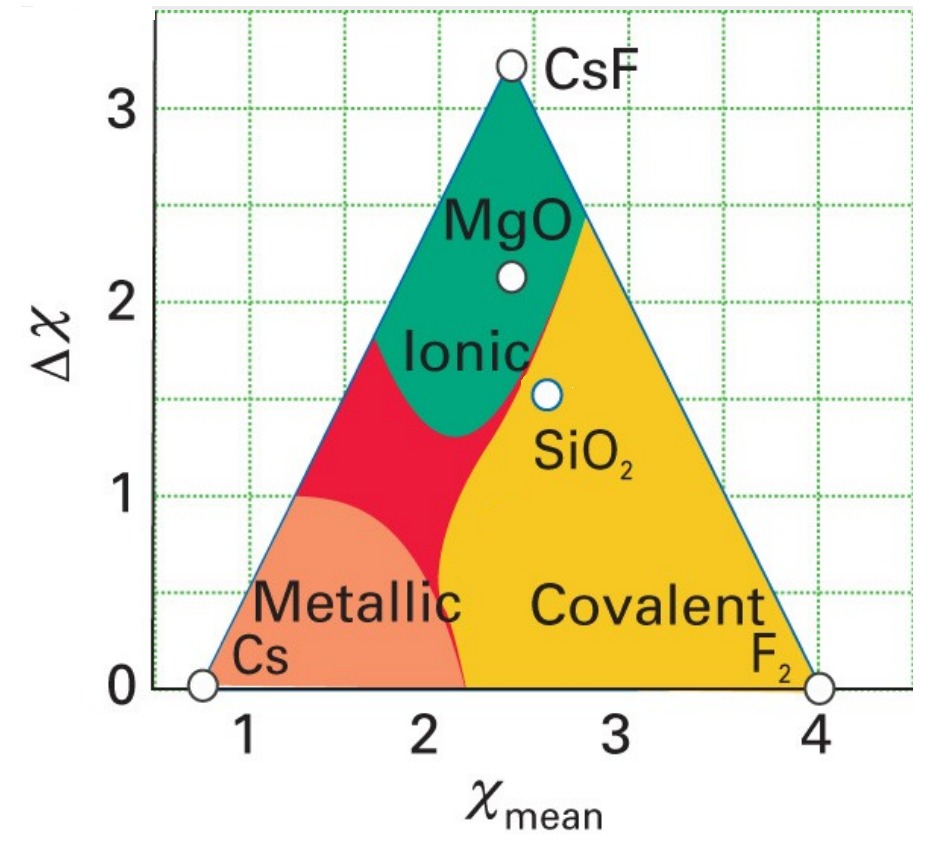ケテラーの三角形を用いると、
例えば、
$\rm MgO$は$Δχ=3.44-1.31=2.13$で$χ_{\rm mean}=2.38$なので、イオン結合(Ionic bond)に分類でき、
$\rm SiO_2$は$Δχ=3.44-1.90=1.54$で$χ_{\rm mean}=2.67$なので、共有結合(Covalent bond)であると分類できます。
電気陰性度で区別しているため、当然この三角形の頂点はそれぞれ、電気陰性度の最小値の元素と最大値の元素で構成されます。
ポーリングの電気陰性度の最小値はセシウム$\rm Cs$の$0.79$です。
ポーリングの電気陰性度の最大値はフッ素$\rm F$の$3.98$です。
よって、
イオン結合性側の三角形の頂点はフッ化セシウム$\rm CsF$で、
共有結合性側の三角形の頂点はフッ素$\rm F_2$で、
金属結合性がわの三角形の頂点は金属セシウム$\rm Cs$となります。
参考）
シュライバー無機化学 上 p69