ヤーン・テラー効果は一般に非直線分子は縮重した電子状態では安定で存在することができないというものです。
つまり、金属イオン錯体は完全な四面体や八面体ではなかったりするよということを表しています。
ヤーン・テラーの効果の例
ハロゲン化銅(Ⅱ)を例に見てみましょう。6配位のCu2+に6つのハロゲンが八面体型の配置で配位します。この時、このハロゲン6つがすべて同じであってもz軸方向に配位する2つのハロゲンと銅の結合距離は残り4つのハロゲンと銅の結合距離より長くなります。実際の数値は以下のようです。
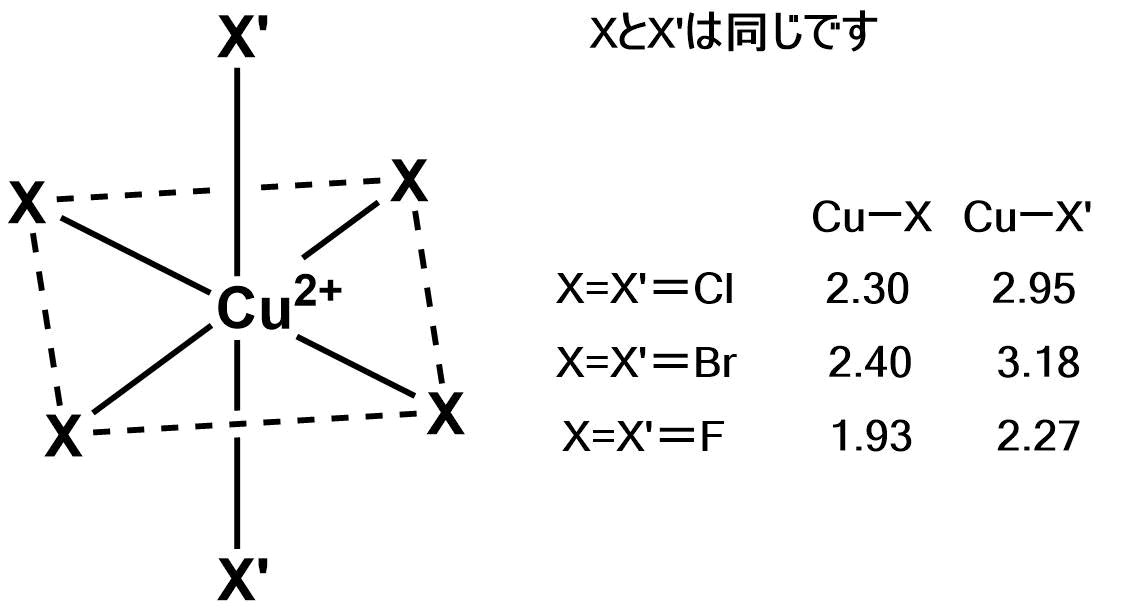
なぜこのようなことが起こるかを考えるためにCu2+のd軌道を考えます。このときeg軌道に一つ空きがあります。なので$d_{x^2-y^2}$に電子が2つ、$d_{z^2}$に電子が1つ入る場合と$d_{x^2-y^2}$に電子が1つ、$d_{z^2}$に電子が2つ入る場合の二通りが考えられます。
仮に、銅のd軌道においては後者が採用されると仮定します。つまり$d_{x^2-y^2}$に電子が1つ、$d_{z^2}$に電子が2つ入る場合ですね。このとき、z軸方向の電子密度が高くなるので、x軸及びy軸方向の4つの配位子よりもz軸方向の2つの配位子のほうが$Cu^{2+}$の電荷が電子によって遥かに多く遮蔽されることになります。そのため、z軸方向の配位子はより遠く離れようとします。
これは実際のデータに合っていますので、実際にハロゲン化銅(Ⅱ)にに於ける銅のd軌道においては$d_{x^2-y^2}$に電子が1つ、$d_{z^2}$に電子が2つ入っているという仮定が正しかったといえます。(銅はこの歪み方を取ります)
ここで前者であった場合、つまり、$d_{x^2-y^2}$に電子が2つ、$d_{z^2}$に電子が1つ入る場合は逆に、x軸方向とy軸方向の4つの配位子の結合距離のほうが短くなります。これはハロゲン化銅(Ⅱ)に関して言えば当てはまらない事になりますね。
このようにどのような歪み方になるかは予想することが非常に難しく、実際のデータを図るしかないのですが、いずれにせよ、このような歪み「ヤーン・テラー効果」はこのように説明することができます。
ヤーン・テラー効果が起こる錯体は3種類
ヤーン・テラー効果が現れるのは
\begin{eqnarray}
6配位八面体型錯体& \ &高スピン型&& \rm d^{4}配置\\
6配位八面体型錯体& \ &低スピン型&&\rm d^7配置 \\
6配位八面体型錯体& \ &&&\rm d^9 配置 \\
\end{eqnarray}の三種類のみです。この3つに共通する特徴は、$e_g$軌道に対が無い電子が1個存在するということです。
正方ひずみが現れると、二重に縮重している$e_g$軌道が分裂し、$d_{xy}$軌道が安定に、$d_{x^2-y^2}$が不安定になります。なので、$e_g$軌道に対が無い電子が1個存在すると、重心則を考慮した際の合計のエネルギーが減少するので、安定化します。
$t_{2g}$に関しては、重心則を考慮すると、合計のエネルギーに変化はありません。
そのため、全体のエネルギーは減少します。
また、$t_{2g}$の安定化効果が得られる$\rm d^2$配置などでもヤーンテラー効果が起こりそうですが、配位子方向に張り出している$e_g$軌道と異なり、$t_{2g}$軌道は配位子の間に広がっているため、$t_{2g}$軌道に基づくヤーンテラー効果は小さくなります。これと同じ理屈で、四面体型錯体においてもヤーンテラー効果によるひずみはほとんど認められません。
高スピン状態のCr2+を例に取ってヤーン-テラー効果を説明せよ。
Cr2+の電子配置は[Ar](3d)4であるので、八面体場中の高スピン状態であれば電子配置は$(t_{2g})^3 (e_g)^1$ であり、下の図のようになる。
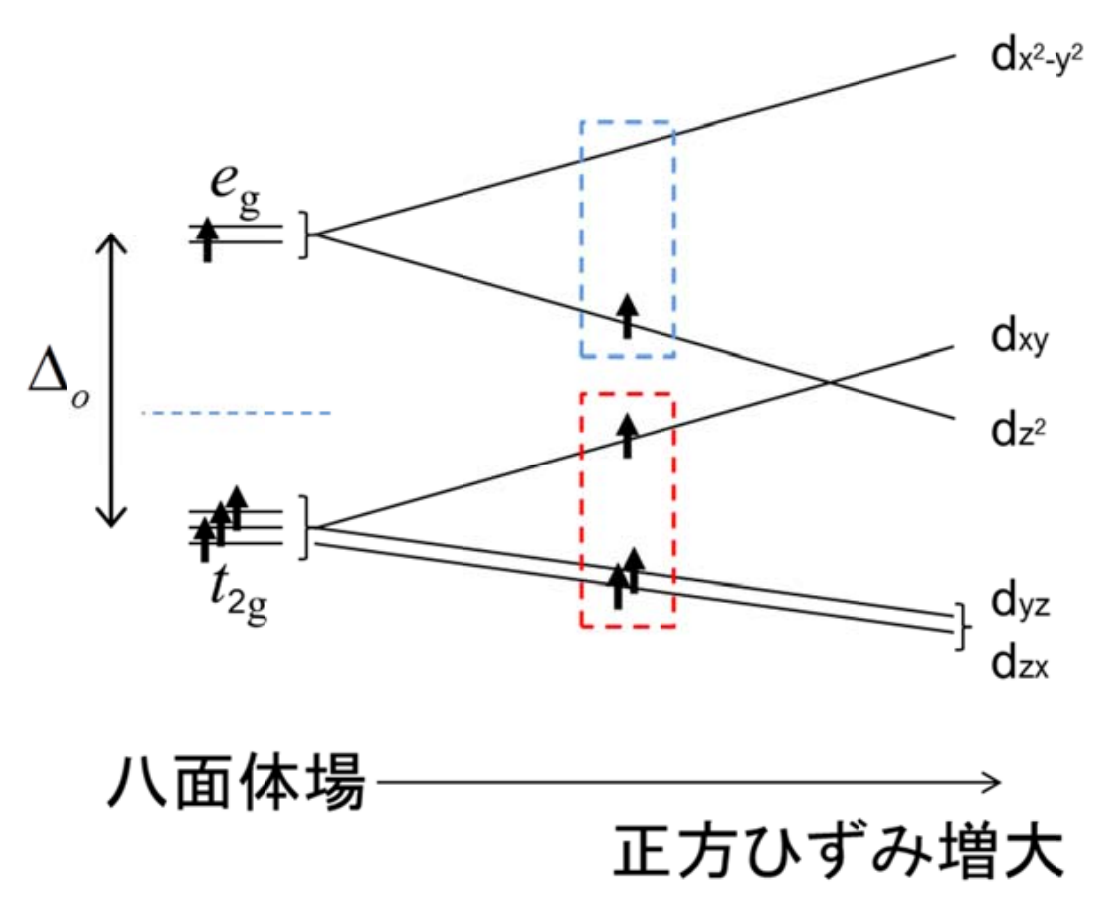
もし正方場でひずみが現れると、$t_{2g}$に配置された3つの電子は赤枠に示すように1つが不安定な準位に、2つが安定な準位に配置されるが、重心則を考慮すると合計のエネルギーに変化はない。
一方で、$e_g$に配置された一つの電子は青枠に示すように正方ひずみによってより安定なエネルギー準位に再編成され、不安定化する電子が存在する電子が存在しないため、八面体場中にいるよりも安定な状態になる。このように安定な状態になるために自発的にひずみを生じる効果をヤーン・テラー効果という。
参考:
コットンウィルキンソンガウス 基礎無機化学 p518 p519
無機・分析化学演習 p116