このページでは二次元マーデルング定数の求め方を説明します。
イオン-イオン間の静電的相互作用によるエネルギーの総和$E$は結晶における最隣接原子間距離を$R$ 、イオンの価数を$Z$ 、素電荷を$e$ として
$$E=-α\f{Z^2e^2}{R}$$と表すことができます。
このとき、定数αがマーデルング定数といわれるもので、今回求める2次元結晶のマーデルング定数の場合、すべての中心イオンとそれ以外のイオンの組において、中心イオンから最近接の原子距離を1としたときの各イオン同士の相対距離を反比例させたものをイオンの符号も勘案して合計したものになります。
二次元マーデルング定数を求めよう
マーデルング定数は距離が短いイオン同士の組の影響を強く受けるので、中心イオンから距離の短いイオンのから順に遠いイオンの組を足していきます。実際計算していくと、次のようになります。$$α=\f{4}{1}-\f{4}{\sqrt 2}+\f{4}{2}-\f{8}{\sqrt 5}+\f{4}{2\sqrt 2}・・・$$しかし、このように規則性もないまま計算していくのには限界あります。
では、その規則性を探してみます。
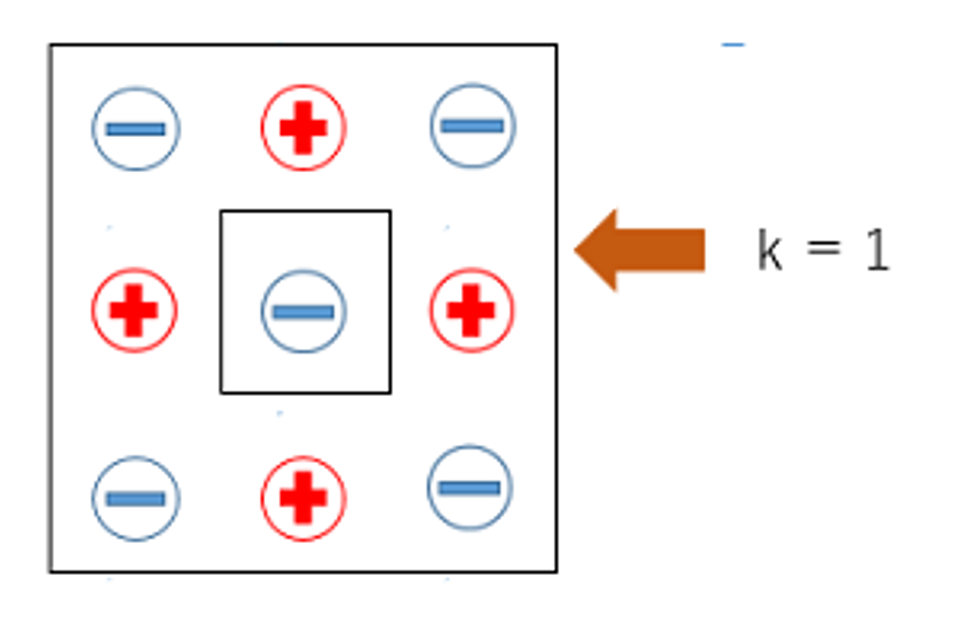 その規則性は以下のようになります
その規則性は以下のようになります
このとき、各外周において、次の規則が見出せる。
・その外周における最大の距離と最小の距離のイオンの組み合わせは4組ずつ(×方向と十字方向)存在し、それ以外の組は8組ずつ存在する。
この上の規則を考慮し、各外周における合計の値を出し、それを1番目からn番目まで合計し、その無限極限をとることで、理論上それは二次元マーデルング定数と同値になります。
ここで外周の距離の種類を$l$とすると、以下のような関係が成り立ちます。
$$l=k+1$$よって、上述の規則性に注目すると、二次元のマーデルング定数は変数$k$,$l$を用いて以下のように記述できます。
$$α=\lim_{n→∞}\sum^{n}_{k=1}\left\{ \sum^{k+1}_{l=1}(-1)^{k+l+1}\f{8}{\sqrt{k^2+(l+1)^2}}-(-1)^k \f{4}{k}-\f{4}{k\sqrt{2}} \right\}\tag1$$
コンピュータで計算してみよう
上の$(1)$式を実際にマセマティカで計算してみました。ただ、$n$は無限大で計算することはできないため、有限の$n$で計算を行うことになります。
マセマティカに$n$に$1000$を代入して計算したところ、マーデルング定数は$1.614$ほどになりました。($n$に$100$を代入した場合は、$1.608・・・$になりました。)
まとめ
以上により、二次元格子結晶におけるマーデルング定数の近似値を計算することができました。
二次元格子結晶は1次元格子結晶より安定で、3次元格子結晶より不安定です。
これを踏まえると、
1次元の、3次元のマーデルング定数はそれぞれ$2\log2$,$1.747$(${\rm NaCl}型です$)で、
$$2\log2\qquad<\qquad1.614\qquad<\qquad1.747$$であるため、このことから、値1.614は事実と矛盾しない妥当なものだということができます。
また、$n=100$の時の値と、$n=1000$の時の値を比べると、後者の方が大きいことから、無限級数は増加する傾向にあると思われ、実際の二次元格子結晶のマーデルング定数は1.614より少し大きい値になると予想できます。