$$\newcommand\vm{{V_{\rm m}}}\newcommand\vms{{V\stst_{\rm m}}}
$$
まず完全気体の場合は$Z=1$ですので、
$$p\vm=RT×1$$となります。
しかし、実在気体ではこの$Z$が変動してきます。
ではこれを表すにはどのような方法があるでしょうか。
$Z$は圧力$p$によってある傾向をしめします。
低圧・・・・・$Z≈1$
中間の圧力・・$Z<1$
高圧・・・・・$Z>1$
つまり、実在気体において、圧力因子$Z$は圧力の影響を受けるということです。
では、実在気体の$Z$を$p$の関数で表せないか。
と思いつきます。
そこで、圧縮因子$Z$を
$$Z=1+Bp+ Cp^2+Dp^3…… $$
とおいてやって、「実際どんな$p$の関数になるかわからないけど$p+p^2+p^3……$ の形で表して、$B$や$C$などの係数を決めることができれば近似できるだろう」と考えます。
ではこれを
$$p\vm=RTZ$$
に代入してやると、
$$p\vm=RT(1+Bp+ Cp^2+Dp^3……)\tag1$$
となります。これをビリアル状態方程式といいます。
そして、係数$B,C,D⋯⋯$は温度に依存する係数で第2、第3、第4・・ビリアル係数といいます。
もちろん、第1ビリアル係数は理想気体の1です。
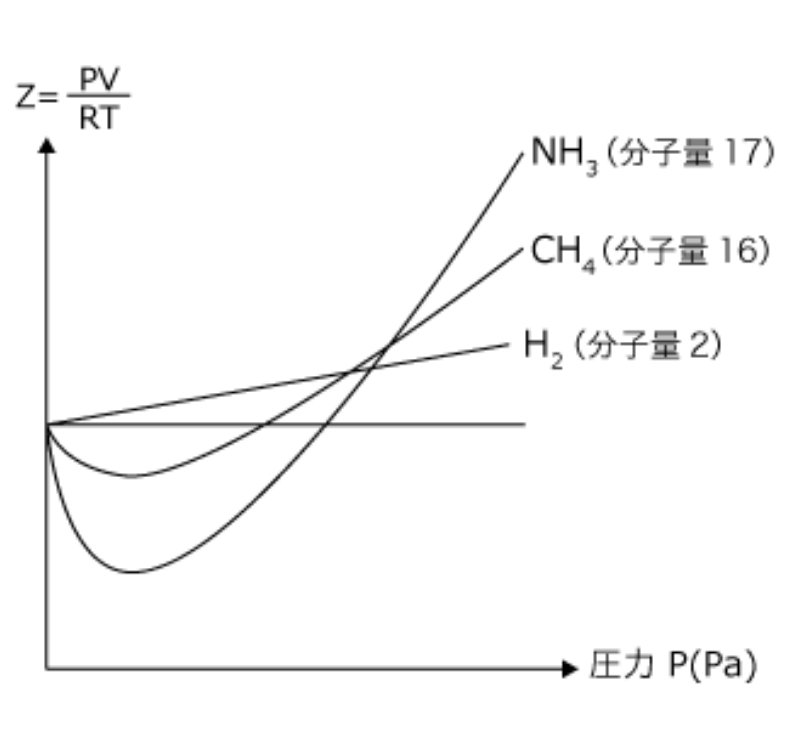
さて、よくこんなグラフを見かけませんか?
(図引用:https://www.sidaiigakubu.com/examination-measure/chemistry/41/)
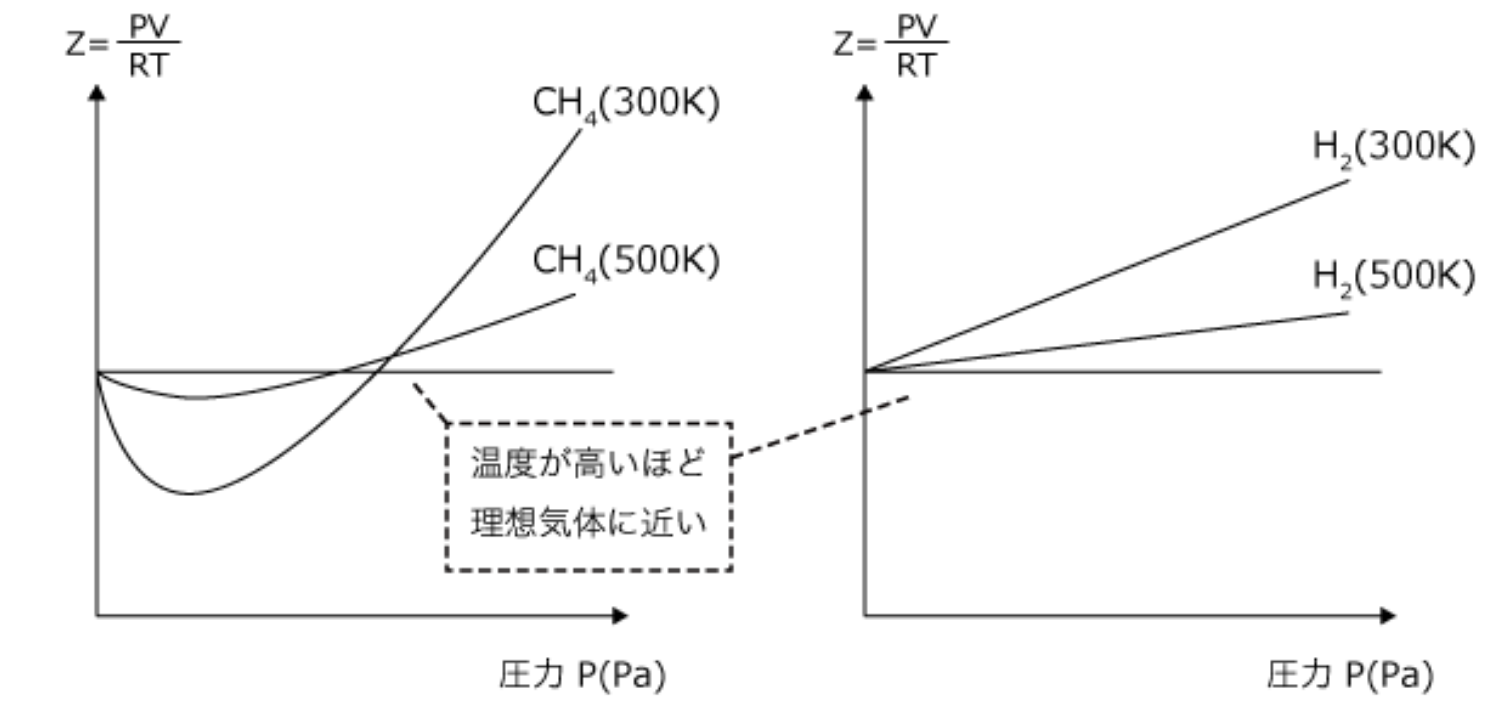
これは$Z-p$グラフです。このグラフ曲線は温度は一定にし、圧力を変えたときのZの変化を表しています。(温度が変わるとグラフも変わります)
さて、これと第2ビリアル係数を関係づけてみましょう。
$p→0$の極限においては$p^n(n>2)$以上は二次近似以上になるため、
第1ビリアル係数と第2ビリアル係数以外は考慮しなくても良いことになります。
よって、$(1)$式より$p→0$の極限において、
$$\b p\vm&=&RT(1+Bp)\\
\f{p\vm}{RT}&=&1+Bp\\
Z&=&1+Bp\\
\df{Z}{p}&=&B(両辺をpで微分)
\e$$
これからわかるように、第2ビリアル係数$B$は$p→0$の極限における$Z-p$グラフの傾きを表していることがわかります。
それではさきほどの図の$p→ 0$付近を見ます。
そうすると、水素では傾きが正になっているのに対して、メタンの場合は負になっています。
つまり、第2ビリアル係数は水素では正、メタンの場合は負になっているということです。
次は、なぜ、ビリアル係数の符号が変わってくるか考えてみましょう。
ここで、実在気体と理想気体の違いをチェックしましょう。
この2点でした。
・分子間力が働く。
・分子自体に体積が存在する。
まず、分子間力が働くと$Z$の大きさは小さくなります。
引力が働いて、気体がコンパクトにまとまり、1mol当たりの気体が占める体積が減少するためです。
一方、分子自体に大きさが存在すると$Z$の大きさは大きくなります。
単純に分子自体が占める体積が加算されて、1mol当たりの気体が占める体積が増加するためです。
そこで、水素とメタンの違いです。水素は常に傾きが正ですね。つまり、分子間力は非常に弱く、常に分子自体が占める体積による影響の方が大きくなるため、$Z$は1以上です。しかも、高圧になればなるほど分子自体の体積による影響は大きくなるので傾きも正になっています。
ではメタンではどうでしょうか?これもまず定圧部分では分子間力による影響の方が分子自体の体積による影響より大きいため、$Z$が減少しますが、その後高圧になると、やはり分子自体の体積による影響の方が大きくなるため、$Z$が増加していく。と説明できます。
要は、その圧力において、分子間力の影響と分子自身の体積による影響が相対的にどちらの方が大きくなるかによって決まる。といえます。
では最後に、以上を踏まえて練習してみましょう。
例題)273℃より温度が低い場合、$p→0$付近の水素の第2ビリアル係数は減少するか?増加するか?理由も含めて100字程度で答えよ。
この場合、温度が低いと分子の速さが低下し、分子の運動エネルギーが減少するため、相対的に分子間引力が大きくなります。(分子間引力は温度によらないため)
つまり、分子間引力の影響が大きくなるため、正だった傾きの大きさはだんだん減少していき、0に近づく方向になります。そのため、傾きを表している第2ビリアル係数も正から減少する方向へと変化する、つまり減少する。といえます。これを100字で説明してみます。
解答例)
高圧においては分子自身の体積による$Z$の増加の傾向が強いが、低圧付近では分子間引力により、$Z$の増加が緩和される。よって温度が減少すると分子同士が引力でとらえやすくなり、分子間引力の影響が大きくなるため、減少する。
参考:アトキンス 物理化学 上 第8版 pp.14~16