いづれの結晶粒も再結晶が進展する全時間$t$に対して、潜伏期間$τ$があるとすると、結晶粒の半径$D$は
\begin{eqnarray}
D&=&G(t-τ) \\
\end{eqnarray}
で表すことができると仮定する。
そして、一つ一つの再結晶粒に着目すると、その体積$V$は球を想定しているので、結晶粒半径$D$の3乗に比例する。
\begin{eqnarray}
V&=&fG^3(t-τ)^3 \\
f&=&形状因子(球の場合なのでf=\f{4}{3π}) \\
\end{eqnarray}
初めに核生成して成長してしまったために、核生成が起こらなかった場合も存在する。そのため以下の考えが必要になる。
核の生成による、再結晶の進展とともに核同士の衝突が生じる。核同士のの衝突がないと仮定した場合の核の数$\d n’$と実際に核の数$\d n$との関係は、
\begin{eqnarray}
\dot{N}\d τ≡\d n’&=&\d n+\dot{N}X\d τ \\
\d n&=&(1-X)\dot{N}\d τ \\
\f{\d n}{\d n’}&=&(1-X) \\
\end{eqnarray}
ここで、$X$はすでに核生成した体積率で$\dot{N}X\d τ$は幻の再結晶の数。
本来起こったであろう再結晶粒(幻の再結晶粒)まで含めたすべての再結晶粒の体積を「拡張体積」$X_{\rm EX}$と呼ぶことにすると、
\begin{eqnarray}
X_{\rm EX}&=&\int V\d n’=fG^3\int^t_0(t-τ)^3\dot{N}\d τ \\
潜伏期間&τ&について積分すると、 \\
X_{\rm EX}&=&\f{f\dot{N}G^3t^4}{4} \\
よって、\f{\d n}{\d n’}&=&\f{\d X}{\d X_{\rm EX}}=(1-X) であるから\\
X&=&1-\exp\s{-X_{\rm EX}}=1-\exp\s{-\f{f\dot{N}G^3t^4}{4}} \\
\end{eqnarray}
と表すことができる。
これをより一般化するとこの式は
\begin{eqnarray}
X&=&1-\exp\s{-Bt^k} \\
と表すことができる&。& \\
これの両辺&に&自然対数をとると \\
\ln\s{1-X}&=&-Bt^k \\
さらに両辺&に& 自然対数ととると\\
\ln\s{\ln\s{\f{1}{1-X}}}&=&k\ln τ+\ln B
\end{eqnarray}
となる。実験データをこの式に当てはめると、
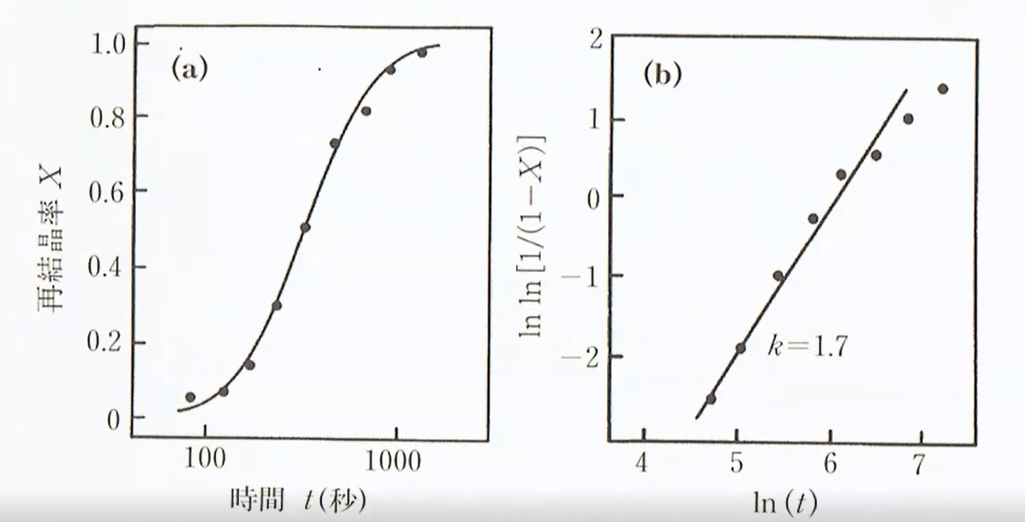
以上のようなプロットが得られる。(a)は再結晶率と焼きなまし時間の関係で(b)はJMAKプロットといわれる。
実験的に求められるのは再結晶率と熱処理時間である。そのため、傾きから$k$を求めることができ、この$k$の数値から以下のことがわかる。
\begin{eqnarray}
3&≦&k≦4→ 3次元成長 \\
2&≦&k≦3 →2次元成長 \\
1&≦&k≦2 →1次元成長 \\
\end{eqnarray}
つまり、このJMAKプロットから成長様式がわかる。