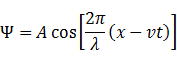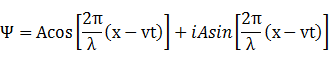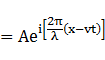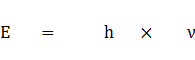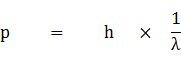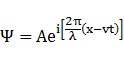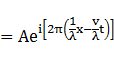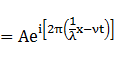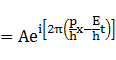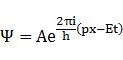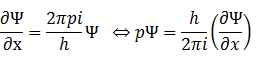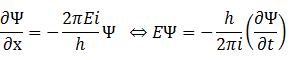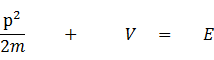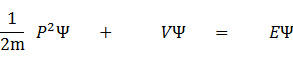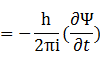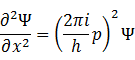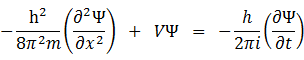注意!)化学科の大学1年生の個人的な覚書です。来た人はブラウザバック推奨!
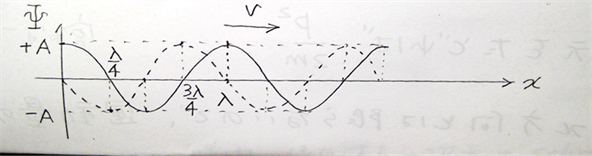
方向に速さvで運動する振幅Aの波
①式
一方、Ψの変化量に着目すると(つまり、xで微分すると)点線のような波になる。![]()
の位置では、Ψ=0となるが、その時変化量は最大となる。これは位置エネルギー→運動エネルギーへと変換されたとみなすことができる。この運動エネルギーに相当する部分が①では無視されているので、
②式
以下の2つの式は電子の粒子性と波動性をつなげる式である。
(右辺が粒子性、左辺が波動性)
・(時間変化)E・・(エネルギー)h・・(プランク定数)ν・・(単位時間当たりの振動数)
アインシュタインの式
・(空間分布)p・・(運動量)h・・(プランク定数)1/λ・・(単位長さ当たりの波数)
ドブロイの式
②式は
よって
③式
運動量p、エネルギーEで+x方向に運動する電子の波動関数は③であらわされる。以下の式も成立。
(運動エネルギー)+(位置エネルギー)=(全エネルギー)
より
③式をxで2回微分すると、
より
代入すると
④式
この④式が時間に依存する1次元のシュレディンガー方程式である。