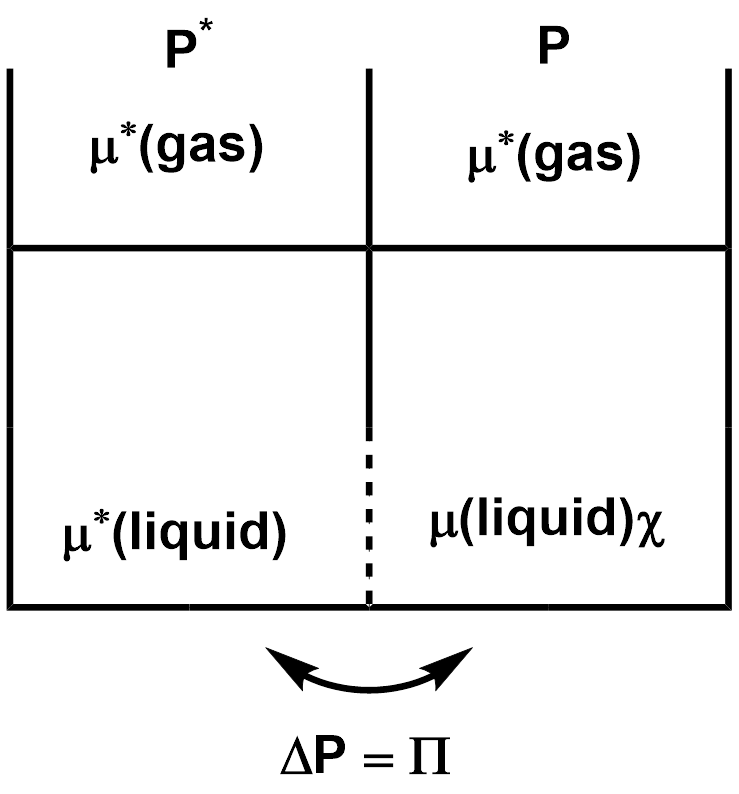
浸透は、溶液と純溶媒を半透膜で隔てた時い、純溶媒側から溶液の方に向かって溶媒分子が浸透していく現象です。ここで半透膜とは、溶媒分子(水分子など)を通すが、溶質分子は通さない性質を持った膜のことです。このような現象が起こるのは「溶液中の溶媒分子の化学ポテンシャルは、純溶媒中の溶媒分子に比べて必ず化学ポテンシャルが低いため、化学ポテンシャルの高い方から低い方へ溶媒分子が移動するため」と説明できます。
溶媒側に大気圧を加えて、追加の圧力$Π$をかけ、溶液側の圧力を高めることで、溶媒分子が溶液の圧力を高めることで、溶媒分子が溶液側へ浸透する圧力と釣り合わせ、溶媒の浸透を抑えることができます。圧力$Π$は、溶媒分子が半透膜を介して溶液側へ浸透してくる圧力と等しいと考えられます。この圧力$Π$を浸透圧と言います。浸透圧を計ることで、溶液中の分子、特に巨大な分子のモル質量(分子量)を計測することができます。
化学ポテンシャルを用いて浸透圧を定量的に求めてみます。
溶液側の溶媒分子のモル分率を$χ_{溶媒}$とすると釣り合いの条件は
$$μ^*_{純溶媒}(P)=μ_{\rm 溶媒in溶液}(χ_{溶媒},P+Π)$$
と表されます。ここで、上の式の左辺は純溶媒側の溶媒分子の化学ポテンシャルを、右辺は溶媒側側の溶媒分子の化学ポテンシャルを表します。この右辺は以下のように表すこともできます。
$$μ_{\rm 溶媒in溶液}(χ_{溶媒},P+Π)=μ^*_{P+Π}+RT\ln χ_{溶媒}$$
ここで温度一定であれば$\d T=0$なので、$V_{\rm m}$を溶媒
の部分モル体積とすると、$\d μ=V_{\rm m}\d P$が成り立ちます。ここでこれを積分すると、
$$μ^*_{純溶媒}(P+Π)=μ^*_{純溶媒}(P)+\int^{P+Π}_{P}V_{\rm m}\d P$$
となります。したがってこの圧力範囲で$V_{\rm m}$が一定であるとすると、上式は
$$μ^*_{純溶媒}(P+Π)=μ^*_{純溶媒}(P)+V_{\rm m}Π$$
となる。ここで以下の式が成り立ちます。
$$0=V_{\rm m}Π+RT\ln χ_{溶媒}$$
ここで、$χ_{溶媒}=1-χ_{溶質}$,かつ$χ$が十分小さいとき$\ln(1-χ)$は$-χ$と近似できるので、希薄溶液において以下の関係が成り立ちます。
$$RTχ_{溶質}≈V_{\rm m}Π$$
希薄溶液であるので、$n_{溶媒}>>n_{溶質}$です。そのため、
$$n_{溶媒}V_{\rm m}+n_{溶質}V_{\rm m溶質}≈n_{溶媒}V_{\rm m}$$
また、以下の近似式も成り立ちます。
$$χ_{溶質}=\f{n_{溶質}}{n_{溶媒}+n_{溶質}}≈\f{n_{溶質}}{n_{溶媒}}$$
ここで、以上の近似式を用いて式を整理すると、
$$n_{溶質}RT≈VΠ$$
となります。もしくは、溶質の体積モル濃度を用いて、
$$Π≈\f{n_{溶質}}{V}RT=[C_{溶質}]RT$$
という近似式を得ます。質量を計った溶質を体積$V$の溶媒に希薄溶液としての条件を満たすように少しだけ溶かし、その浸透圧を測れば溶質の分子量が測定できます。これは高分子など、分子量が測定しにくい巨大分子の分子量を決定するのに有効な方法となります。