 $\newcommand\R{{\rm R}}\\\newcommand\I{{\rm I}}\\\newcommand\P{{\rm P}}$
$\newcommand\R{{\rm R}}\\\newcommand\I{{\rm I}}\\\newcommand\P{{\rm P}}$
$\newcommand\i{{[\rm I]}}\\\newcommand\r{{[\rm R]}}\\\newcommand\p{{[\rm p]}}$
(1)-(a)の解説
$$\b \df{[\R]}{t}&=&-k_1[\R]\tag1\\
\df{[\I]}{t}&=&k_1[\R]-k_2[\I]\tag2\\
\df{[\P]}{t}&=&k_2[\P]\tag3
\e $$
(1)-(b)の解説
$(1)$式より、
$$\b \df{[\R]}{t}&=&-k_1[\R]\\
\f{\d [\R]}{[\R]}&=&-k_1\d t\\
\ln{[\R]}&=&-k_1 t+c(両辺を不定積分、cは積分定数)\tag4\\
\ln{[\R_0]}&=&c((4)式に初期条件を代入)\tag5\\
\ln{[\R]}&=&-k_1 t+\ln{[\R_0]}((5)式を(4)式に代入)\\
\ln{\fp{[\R]}{[\R_0]}}&=&-k_1 t\\
\fp{[\R]}{[\R_0]}&=&e^{-k_1 t}\\
[\R]&=&[\R_0]e^{-k_1 t}
\e$$
$$\b [\I]&=&α_1e^{-k_1t}+α_2e^{-k_2t}\tag6\\
&&(6)式と(1)-(b)の答えを(2)式に代入すると\\
\f{\d \i}{\d t}&=&-k_2\i+k_1\r\tag2\\
α_1(-k_1)e^{-k_1t}+α_2(-k_2)e^{-k_2t}&=&-k_2α_1e^{-k_1t}+α_2(k_2)e^{-k_2t}+k_1\r_0e^{-k_1t}\\
&&e^{-k_1t}の係数を比較すると、\\
-k_1α_1&=&k_1\r_0-k_2\a_1\\
&&※ちなみにe^{-k_2t}の係数を比較しても\\
-k_2\a_2&=&-k_2\a_2\\
&&となり、この式からは何も情報を得ることができません。\\
&&以下、続き、\\
-k_1α_1&=&k_1\r_0-k_2\a_1\\
(k_2-k_1)\a_1&=&k_1\r_0\\
\a_1&=&\f{k_1}{k_2-k_1}\r_0\\
\e$$ $t=0$のとき、$\i=0$なので、これを$(2)$式に代入すると、
$$\i=\a_1+\a_2=0\\
\a_2=-\a_1=-\f{k_1}{k_2-k_1}\r_0$$
(1)-(d)の解説
$$\b
\df{\i}{t}&=&0\\
-k_1\a_1e^{-k_1t}-k_2\a_2e^{-k_2t}&=&0\\
-k_1\a_1e^{-k_1t}&=&k_2\a_2e^{-k_2t}\\
e^{-k_1t+k_2t}&=&\f{k_2\a_2}{-k_1\a_1}\\
-k_1t+k_2t&=&\ln\left(-\f{k_2\a_2}{k_1\a_1}\right)\\
t&=&\f{1}{k_2-k_1}\ln\left(-\frac{k_2\a_2}{k_1\a_1}\right)\\
t&=&\f{1}{k_2-k_1}\ln\left(-\frac{k_2}{k_1}\right)\\
&&(\because \a_1=-a_2)
\e$$ よって、$t_{\rm max}=\f{1}{k_2-k_1}\ln\left(-\frac{k_2}{k_1}\right)$
(※増減表を書くともっと正確な果糖になりますが、ここでは増減表は省略します。)
(1)-(e)の解説
定常状態近似とは$\df{\i}{t}=0$と仮定する近似のことです。
そのため、(1)-(d)の結果をそのまま(1)-(c)で求めた$\i$の式に代入すると$\i_{\rm ST}$を求めることができます。
(1)-(c)より
$$\i=\f{k_1}{k_2-k_1}\r_0e^{-k_1t}-\f{k_1}{k_2-k_1}\r_0e^{-k_2t} $$であるので、これに$t$に(1)-(d)の答えである$t_{\rm max}=\f{1}{k_2-k_1}\ln\left(-\frac{k_2}{k_1}\right)$を代入したものが$\i_{\rm ST}$です
(1)-(f)の解説(未完)
$k_1>>k_2$のときに定常状態近似を用いることができます。
この問題では、2つ条件を挙げる必要があります。
申し訳ありませんが、もう一つの条件がなにであるかはわかりませんでした。
 (2)
(2)
(g)項間交差と内部転換である。項間交差は異なる多重度を持つ状態の間で起こる無放射遷移のことで、内部転換は同じ多重度をもつ状態の間で起こる無放射遷移のことである。
(h)未回答です。
(i)
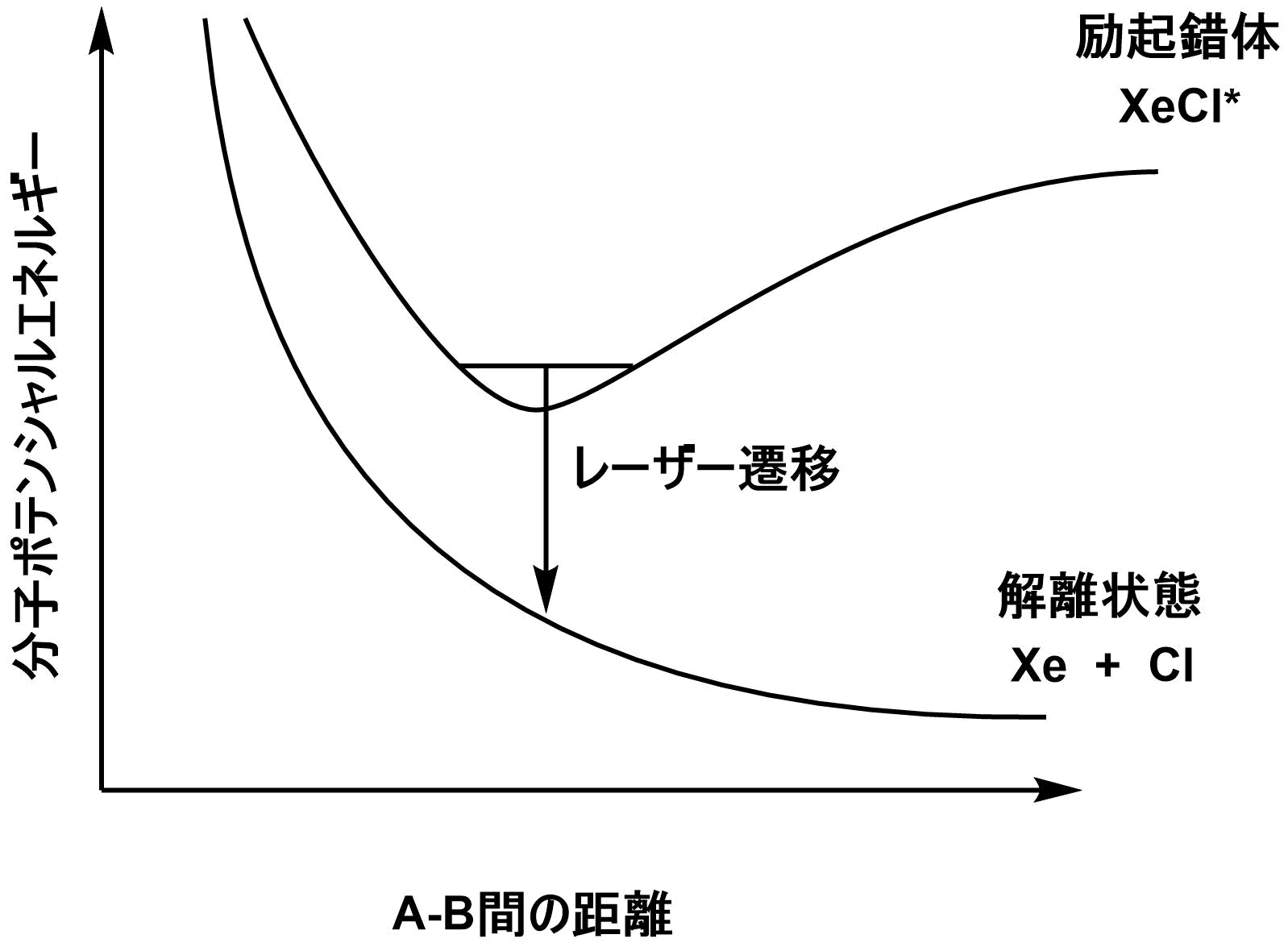
XeCl*という化学種は励起状態にあるときだけ存在することができる。これは、化学種がそのネルギーを失うと、低エネルギーの解離した状態になるためである。つまり、励起錯体は、エネルギーの高い上側の状態でのみ存在できるので、下側の状態にはいかなる占有数も存在しない。そのため、レーザ発振に必要である、「占有数の逆転」を作り出すことができ、適している。
※このような方式で発振するレーザーを励起錯体レーザーといいます。
参考)アトキンス 物理化学 下 第10版 p589
 $\newcommand\R{{\rm R}}\\\newcommand\I{{\rm I}}\\\newcommand\P{{\rm P}}$
$\newcommand\R{{\rm R}}\\\newcommand\I{{\rm I}}\\\newcommand\P{{\rm P}}$ (2)
(2)