ボルツマン分布
ある準位iの存在確率を$P_i$とすると、ボルツマン分布は以下のようなものでした。
$$P_i=\f{e^{-βε_i}}{\sum_ie^{-βε_i}} $$
この分母の部分は分子分配関数とよばれます。
分子分配関数を$q$とすると、
$$q=\sum_ie^{-βε_i} $$もう少し詳しく書くと、
すべての準位について和を取るわけですが、同じ準位をもったものがあるときがあります。(つまり縮退している場合)
このときは$g_i$というものをかける必要が出てきます。
$$q=\sum_ig_ie^{-βε_i}$$
この$g_i$は何かと言うと、縮退度(あるいは縮重度)と言われるものです。
縮退度は同じエネルギ準位に属する状態の数のことです。この縮退度は1以上の自然数です。縮退していない場合、これは1ですので、省略することができます。
また、分子はその準位のボルツマン係数(あるいはボルツマンファクター)と呼ばれます。
この分子分配関数は温度の関数です。なぜなら$β=\f{1}{kT}$だからです。
まず温度を低くしていきましょう。0に近づくと、βは∞に近づきますから、ボルツマン係数は0に近づきます。そうすると、qは$g_0$に近づいていきます。
逆に温度が無限に近づくほど、βは0に近づき、qは∞に近づきます。
分子は一般に、q(分子の状態の数)は無限個あることが普通です。
このように分子分配関数は温度に依存していることが分かります。
分子分配関数が表すものは「系の温度Tにおいて分子が熱的にとりうる状態の数」です。
温度が低くなると、基底状態しか取れませんので、とれる状態の数は基底状態の縮重度と同じになります。
逆に温度が高くなればなるほど、とりうる状態の数は増えていきます。
「熱的」というのは、特定の運動だけにエネルギーを分配することができないということです。エネルギーがいろいろな自由度に分配されるということです。(エネルギー等分配則)
例1)エネルギー準位が一様な非縮退はしご形(無限個の等間隔の非縮退エネルギー準位)のの分配関数を計算しましょう。
このようなエネルギー準位は非現実的なものではなく、2原子分子の調和近似における振動エネルギー準位を考えるときに用いられるものです。
まず、非縮退なので$g_i=1$です。
$$\b
q&=&\sum_ie^{-βε_i} \\
&=&e^{-β・0}+e^{-β・ε}+e^{-β・2ε}+… \\
&=&e^{-β・0}+e^{-β・ε}+e^{-β・2ε}+… \\
&=&1 +e^{-βε}+(e^{-βε})^2+… \\
&=& 1+x+x^2+…(x=e^{-βε}と置いた)\\
&=&\f{1}{1-x}(公比xの等比級数の和) \\
&=&\f{1}{1-e^{-βε}}
\e$$ これのグラフの概形は以下のようになります。ほとんど直線的に増加していく関数であることが分かります。
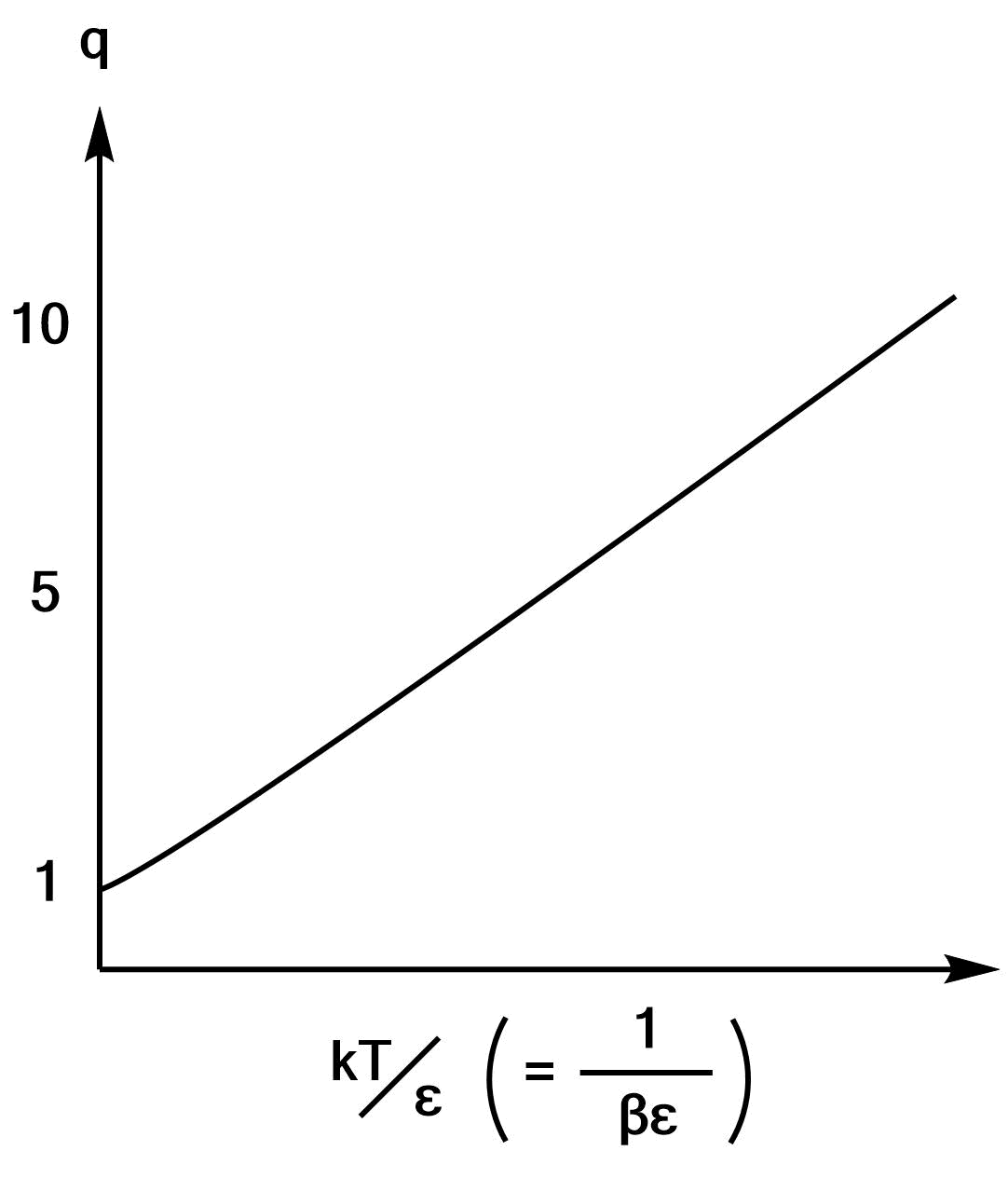
ではつぎの例として、1より簡単な準位が2個しかない状態を考えます。
例2)以下のようなに順位系の$q$を$\f{kT}{ε}$にたいしてプロットしましょう。
$$\b
q&=&\sum_ie^{-βε_i} \\
&=&e^{-β・0}+e^{-β・ε} \\
&=&1+e^{-βε} \\
\e $$この分子分配関数$q$のグラフ概形は以下のようになります。

つまり、2準位系であると、$q$はに2に漸近していくことがわかります。
三準位系でも同じことが言えます。
これから次は占有数について見ていきましょう。
そのそも、$q$はエネルギー$ε_i$の状態にある分子の割合のことです。
例1の場合、
$q=\f{1}{1-e^{-βε_i}}$
であるので、
$$P_i=\f{e^{-βε_i}}{q}=(1-e^{-βε_i})e^{-βε_i} $$各エネルギー順にの占有率の変化は温度が大きくなるほど各準位の占有率は0に近づいていきます。
次は例2の2準位系の占有数の割合の温度変化です.
$$q=1+e^{-βε_i} $$
$$P_0=\f{1}{1+e^{-βε_i}},zP_i=\f{e^{-βε_i}}{1+e^{-βε_i}} $$これはT→∞の極限において、
$$P_0=\f{1}{2}\\
P_1=\f{1}{2}$$
となります。
次は3準位系における$P_i$の温度変化を見ていきましょう。
例に漏れず、横軸を$\f{kT}{ε}$を取ります。
このとき、の分配関数$q$は以下のようでした。
$$\b
q&=&e^{-β・0}+e^{-β・ε}+e^{-β・2ε} \\
&=&1+e^{-βε}+e^{-2βε} \\
\e$$ それでは基底状態の占有数$P_0$、第一励起状態の占有数$P_1$,第二励起状態の占有数$P_2$はそれぞれ以下のようになります。
$$\b
P_0&=&\f{e^{-β・0}}{q} =\f{1}{q}\\
P_1&=&\f{e^{-βε}}{q} \\
P_2&=&\f{e^{-2βε}}{q} \\
\e $$この関数をそれぞれ温度を無限極限まで取る(実際にコンピュータで計算する)と、この3つの関数の値はすべて同じ値になります。そして、その値は2準位系の例と同じように、$\f{1}{3}$です。
次は、最初の例の無限個の等間隔(ε)の非縮退エネルギー準位の占有数の温度変化は以下のようになります。
$$q=\f{1}{1-e^{-βε}} $$$$P_i=\f{e^{-βε_i}}{q}=e^{-βε_1}(1-e^{-βε})$$ この関数をプロットしていくと、$P_0$は単調に減少していき、それ以外はある極大値になるまで増加し、それ以降の温度では減少していきます。また、すべてのエネルギー状態において、任意の温度地点で$P_{i+1}<P_{i}$が成り立っています。
そして、温度の無限極限はすべてのエネルギーの占有数は同じ値に収束していき、それは0です。
(つまりn準位系における温度の無限極限における各エネルギー準位の占有数は$\f{1}{n}$)
次は$\rm I_2$分子における振動エネルギー準位を考えていきます。
25℃における$P_0,P_1P_2$を計算してみます。
$\newcommand\n{\tilde{ν}}$
ここで必要なのは、具体的にエネルギー準位の間隔の値です。いままではεをもちいていました。
このエネルギーを表すのには通常波数で表されます。
振動の波数は$(\n)=214.6[{\rm cm^{-1}}]$($\n$はニューチルダと読みます)
それでは波数と振動数の関係は以下のようでした。
なので、振動数$ν$は以下のようになります。
$$\b
ν&=& c\n\\
&=&3.00×10^8×214.6×10^{2}[{\rm m^{-1}}※単位に注意] \\
&=&6.438×10^{12}[{\rm s^{-1}}] \\
\e $$
よって、
$$\b
ε&=&hν \\
&=& 6.626×10^{-34}[{\rm Js}]×6.438×10^{12}[{\rm s^{-1}}] \\
&=&4.266×10^{-21} [{\rm J}]\\
\e $$
$$\b
βε&=&\f{ε}{kT} \\
&=&\f{4.266×10^{-21}}{1.381×10^{-23}×298} \\
&=&1.036 \\
\e $$
よって、$q$は
$$q=\f{1}{1-e^{-\frac{ε}{kT}}}=1.55 $$また、$\frac{ε}{kT}=\f{1}{1.036}=0.9652$となるので、
各エネルギー準位の占有数は以下のように計算できます。(ここの部分は関数電卓です)
$$\b
P_0&=&\f{1}{q}=0.645 \\
P_1&=&\f{e^{-\frac{ε}{kT}}}{q}=0.229 \\
P_2&=&\f{e^{-\frac{2ε}{kT}}}{q} =0.081\\
\e$$