安定度
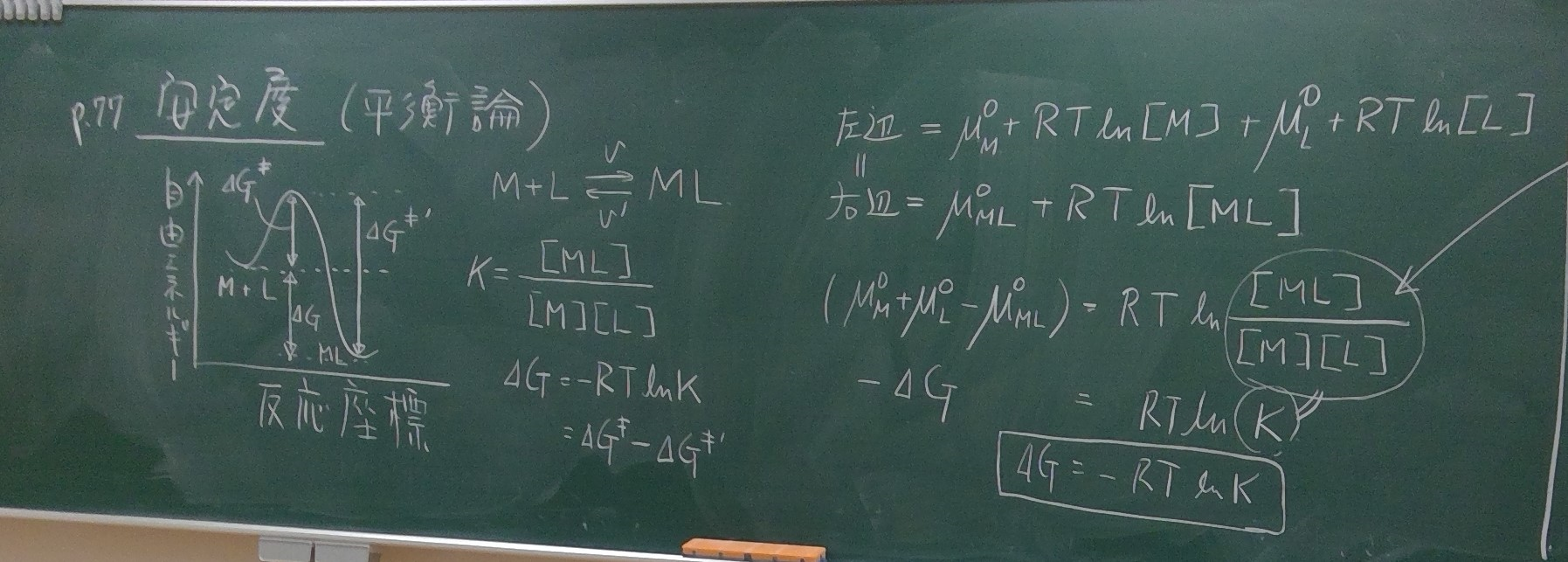
$$\rm M+L⇆ML(上v,下v’)
$$\b
K&=&\rm \f{[ML]}{[M][L]} \\
ΔG&=&-RT\ln K \\
&=& ΔG^{‡}-ΔG^{‡^’}\\
(左辺)&=&μ^{\stst}_M+RT\ln{[\rm M]}+μ^{\stst}_L+RT\ln{[\rm L]} \\
(右辺)&=& μ^{\stst}_{\rm ML}+RT\ln{[\rm ML]}\\
(μ^{\stst}_{\rm M}+μ^{\stst}_{\rm L}+μ^{\stst}_{\rm ML})&=& RT\ln\s{\ln\f{[\rm ML]}{\rm [M][L]}}\\
-ΔG&=&RT\ln K \\
ΔG&=&-RT\ln K
\e
逐次安定度定数
$$\b
\rm M+L&⇆&\rm ML \ K_1=\f{[ML]}{[M][L]}\\
\rm ML+L&⇆& \rm ML_2 \ K_2=\f{[ML_2]}{[ML][L]}\\
\rm ML_{n-1}+L&=& ML_n \ K_n=\f{[ML_n]}{[ML_{n-1}][L]}\\
\e
この$\rm K_n$は逐次安定度定数といい、
$$\rm M+nL⇆ML_n \ β_n=\f{[ML_n]}{[M][L]^n}
のまとめた反応の安定度定数を全反応定数といいます。
もちろん安定度定数にも$β_1からβ_n$まであります。
$$β_1=K_1\\β_2=K_1K_2\\β_n=K_1K_2…K_n
となる。
たとえば、銅アンミン錯体の場合は、配位数4と言われますが、これは$β_4$が$β_5$に比べてとても大きいからです。
銅アンミン錯体の場合は
$$\log K_1=4.25,\log K_2=3.61,\log K_3=2.98,\log K_4=2.24,\log K_1=-0.25
となります。一般に、$K_n>…>K_2>K_1$の順で減少していくのは一般的にそうです。
これは、純粋に、統計上、高次の錯体ほど生成確率が低いためです。しかし、$K_5$は統計的な予想値から大幅にずれて減少します。
また、配位子が配位水と置換すると、中心金属イオンの性質や残りの配位座の環境が変化するために$K$の値が多きくずれることもあります。例えば、$\rm Fe(Ⅱ)$のフェナントロリン錯体では$\log K_1=5.9$,$\log K_2=5.4$,$\log K_3=10.0$です。これは、$\rm [Fe(OH_2)_2(phen)_2]^{2+}$の段階までは高スピンであるのに対し、$\rm [Fe(phen)_3]^{2+}$になると、低スピン型となり、大きな配位子場安定化エネルギーを獲得するためです。また、$\rm Cd(Ⅱ)$と$\rm Br^-$イオンの錯体では$\log K_1=2.3$,$\log K_2=0.78$,$\log K_3=-0.22$,$\log K_4=0.08$であり、これは$\rm CdBr^{2-}_4$イオンになるとき、配位数が6から4に変化するためです。基本的に、カドミウムは亜鉛と同じ族で、$d_{10}$金属です。そのため配位子が配位するときはsやpを用いて、$sp^3$混成軌道を形成します。これが4配位になる理由です。(もちろん$sp^3d^2$をつくって6配位になる場合もありますが)