(1)(a)
$$\b
ΔG(0)&=&2885.9[{\rm cm^{-1}}] \\
ΔG(1)&=&5668.0-2885.9=2782.1[{\rm cm^{-1}}] \\
ΔG(2)&=&8347.0-5668.0=2679.0[{\rm cm^{-1}}] \\
ΔG(3)&=&10923.1-8347.0=2576.1[{\rm cm^{-1}}] \\
ΔG(4)&=&13396.5-10923.1=2473.4[{\rm cm^{-1}}] \\
\e$$
(1)(b)
(1)(c)
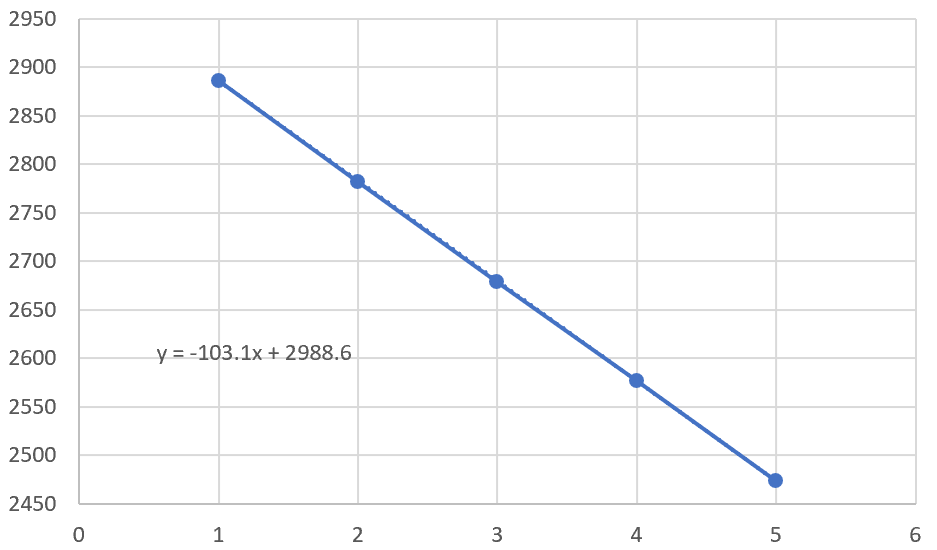
この方法はビルゲ-スポーナーのプロットとして知られる作図法である。
解離エネルギー$D_0$を求めるには零点準位から解離限界までの間の隣り合う間隔$ΔG(v)$を順次加えていけばよい。
具体的には、上のプロットから得られる直線と$x=1$,$y$軸にの3直線によってできる三角形の面積を計算することで$D_0$の波数単位の値となる。
(1)(d)
上記のプロットにより作られる直線の式を計算すると、$y=-103.1x+2988.6$である。これと$x$軸の交点の$x$座標は$v≒29$なので、これと三角形の面積は、
$$2885.9×(29-1)÷2=40402.6≒4.04×10^{4}$$となる。
したがって、$\rm HCl$の解離エネルギーは$D_0=4.04×10^{4}{[\rm cm^{-1}]}$程度であると推定される。
(1)(f)
$D_e$と$D_0$の間には、$D_e=D_0+\f12\tilde{ν}$の関係が成り立つ。
ここで、$\tilde{ν}$は上記の近似直線のy切片に当たる。
よって、
$$D_e=D_0+\f12\tilde{ν}=4.04×10^4+\f12×2988.6=4.19×10^4{[\rm cm^{-1}]}$$