ファンデルワールス力
ファンデルワールス力の距離の６乗$\s{\f1{r^6}}$に反比例します。
①永久双極子-永久双極子相互作用
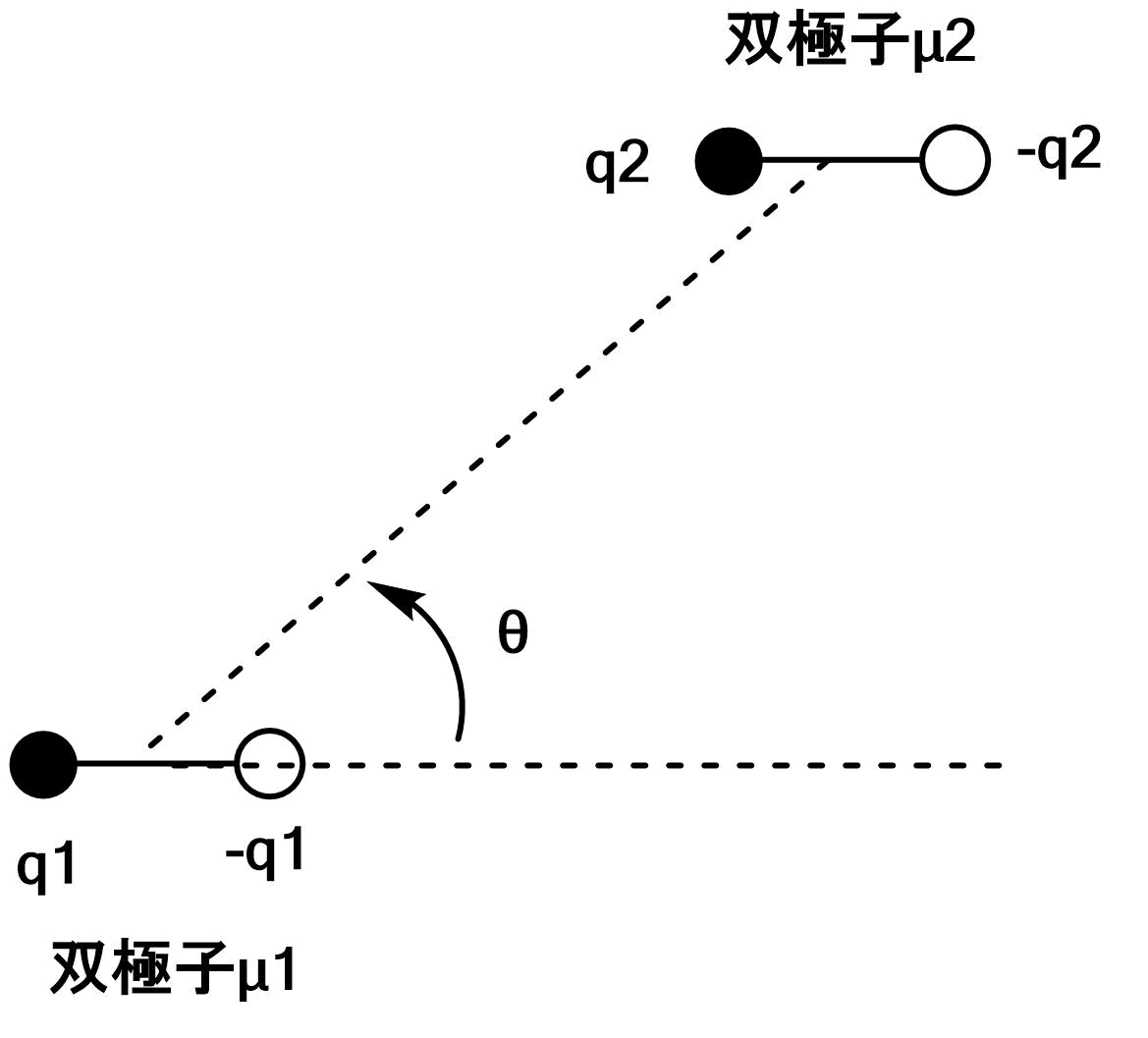
この相互作用は極性分子間で起こる相互作用です。
回転しない双極子同士の相互作用は
$$V=\f{μ_1μ_2f(θ)}{4πε_0r^3}\\
f(θ)=1-3\cos θ $$で表されます。
このとき、
$$\b
θ=0°&⇒&f(θ)=-2 となるため有利な配置になります。\\
θ=\f{π}{2}&⇒&f(θ)=1 となり、不利な配置になります\\
\e $$
ただ、$μ_1$と$μ_2$が自由に回転した時、$V=0$となりますが、実際は両者の配置が互いに依存するため、
$$\overset{ 平均}{<V> }=-\f{C}{r^6}$$ となります。ただし、
$$C=\f{2μ_1^2μ_2^2}{3(4πε_0)^2kT} $$です。これはキーサムの相互作用と呼ばれています。
永久双極子をもつ分子同士の相互作用は以上です。ただし、物質の中には、永久双極子を持たないキセノンのようなものもあります。それも、外部の電場によって引き起こされる誘起双極子を持ちます。次は、永久双極子と誘起双極子の相互作用を考えます。
②永久双極子ー誘起双極子の相互作用
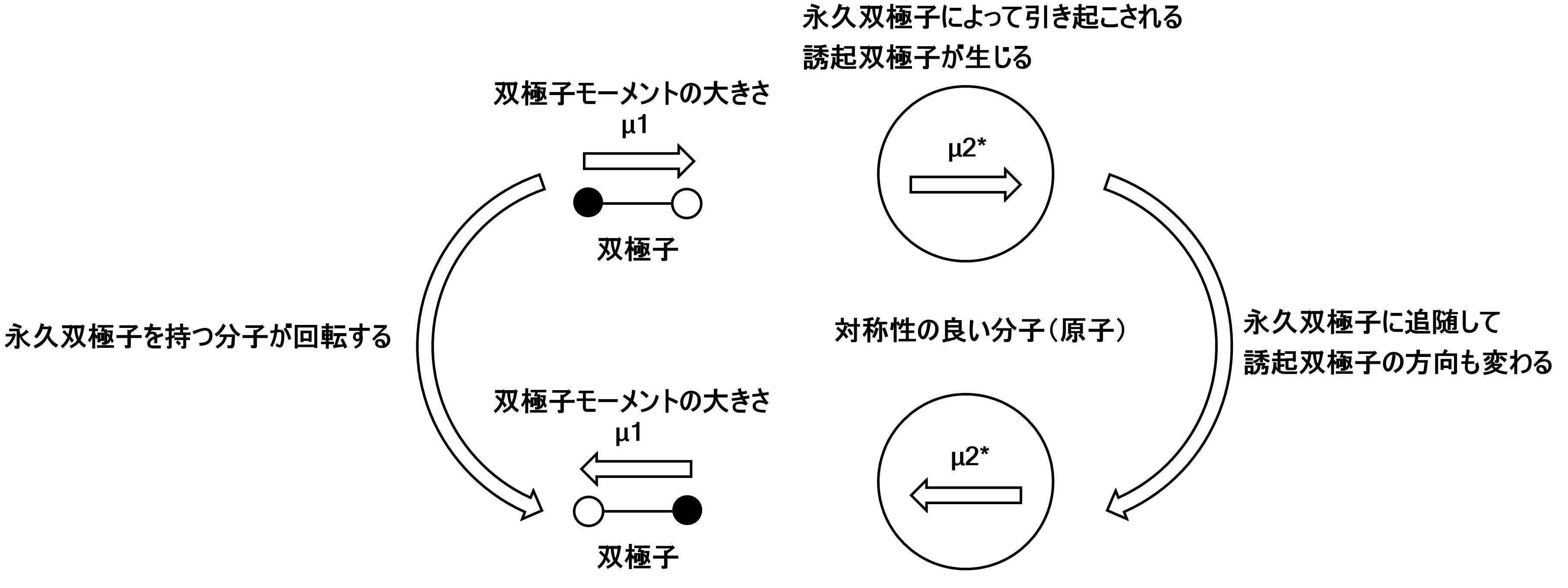
これは、極性分子間と、無極性ー極性分子間で起こる相互作用です。
このときも①と同じように
$$\overset{ 平均}{<V> }=-\f{C}{r^6}$$ となります。
ただし、$C$が異なり、
$$C=\f{μ_1^2α’_2}{4πε_0} $$です。$α_2’$は分極率です。これが①と異なるのは、温度の項が入っていないということです。つまり、この相互作用は温度に依存しません。
次はどちらも永久双極子を持っていない場合です。
③誘起双極子ー誘起双極子同士の相互作用
この相互作用は「分散相互作用」や「ロンドン相互作用」とも言われるもので、極性分子間、無極性分子ー極性分子間、無極性分子間いずれでも起こる相互作用です。
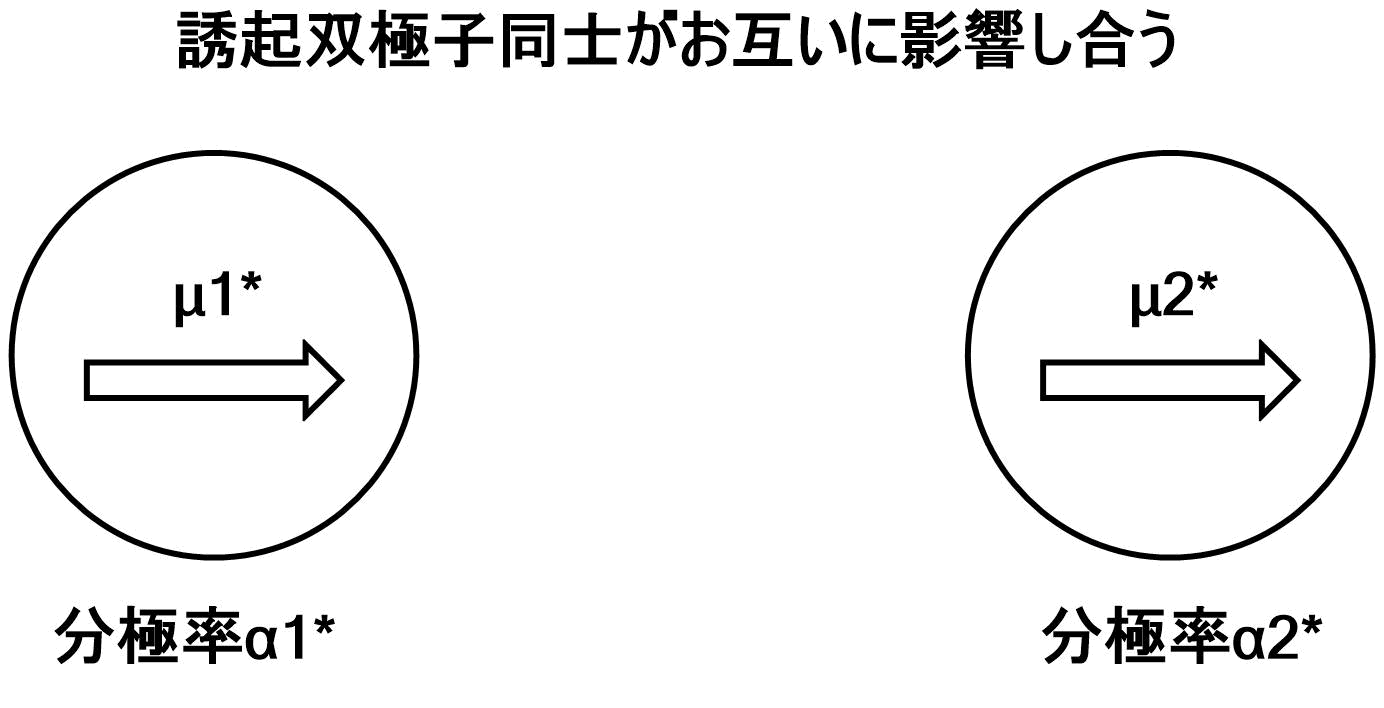※図では、対称の良い無極性分子をイメージしていますが、別に極性があってもこの相互作用は働きます。
そして、この相互作用も①や②と同じように、距離の６乗に反比例します。
$$\overset{ 平均}{<V> }=-\f{C}{r^6}$$ ただし、
$$C=\f32α’_1α’_2\f{I_1I_2}{I_1+I_2} $$です。これは、$α’$は分極率です。そして、$I_1,I_2$は分子１、２のイオン化エネルギーです。この式は「ロンドンの式」と呼ばれています。
以上３つがおもなファンデルワールス力の内訳です。
他にも知られている相互作用はあります。以下に参考として、記述します。
参考)３個以上の分子同士の相互作用
３個の閉殻原子の全分散エネルギーが知られています。
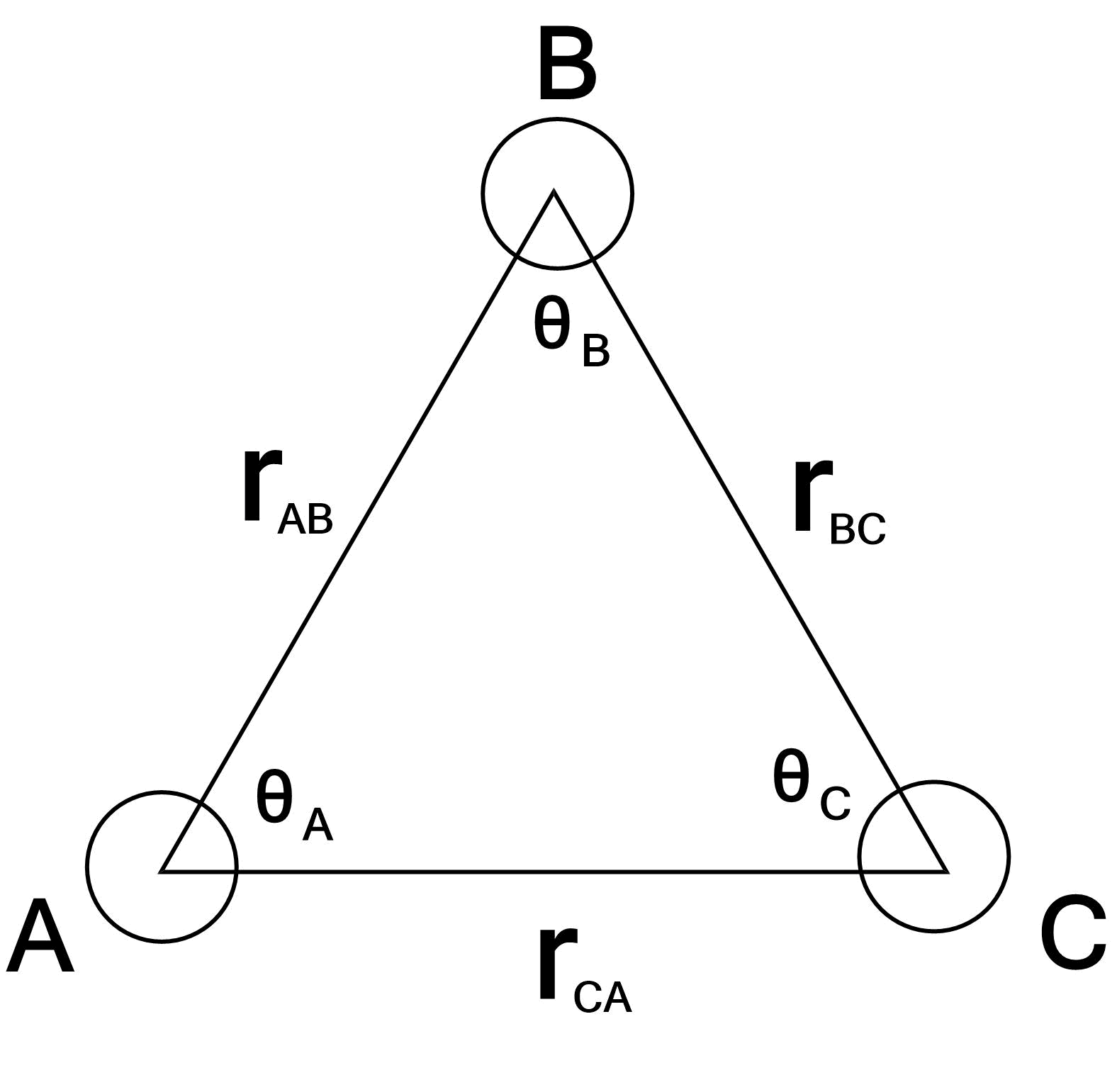$$\overset{ 平均}{<V> }=-\f{C_6}{r_{\rm AB}^6}-\f{C_6}{r_{\rm BC}^6}-\f{C_6}{r_{\rm CA}^6}+\f{C’}{(r_{\rm AB}r_{\rm BC}r_{\rm CA})^3} $$です。ただし、
$$\b
C’&=&a(3\cos θ_{\rm A}\cos θ_{\rm B}\cos θ_{\rm C}+1) \\
a&=&\f34 α’C_6\\
\e $$これはアクシロイドーテラーの式といいます。
(Axilrod-Teller Formula)
この分野とはあまり関係ありませんが、このテラーは「水素爆弾の父」として知られている「Edward Teller」です。Edward Tellerは化学にも大きな業績を残しており、ヤーンーテラー効果なども彼の業績です。