H31 物理化学分野1

31Hの化学(専門)の問題はこちら

熱力学の基本式より、

$$\begin{eqnarray} \d F&=&-S\d T- P\d V+\sum_i n_iμ_i\\ このとき&、&T=const,V=const、さらにi以外考えないとき、\\ \d F&=&n_iμ_i\\ μ_i&=&\ddp{F}{n_i}_{T,V,n_i}\\ \end{eqnarray}$$

となる。よって、答えはアとウ

平衡が成り立っているので、
$$\begin{eqnarray} \d G&=&0\\ μ\d n_{{(\rm gas)}}+μ’\d n_{{(\rm liqid)}}&=&0\\ このとき、\d n_{{(\rm gas)}}&=&-\d n_{{(\rm liqid)}}\\ であるので&,&代入すると\\ μ\d n_{{(\rm gas)}}-μ’\d n_{{(\rm gas)}}&=&0\\ μ-μ’&=&0\\ μ&=&μ’\\ \end{eqnarray}$$
 
より、示された。

おそらく一成分系の化学ポテンシャルが等しいというのが結果ですが、なぜそうなるかというのは調べることができませんでした。

断熱過程なので、熱力学第一法則$\d U=T \d S-P\d V$で$\d U=0$より、
$$\begin{eqnarray} T \d S&=&P\d V \\ \d S&=&\f{P}{T}\d V \\ 理想気体の状態方程式P&=&\f{nRT}{V}を代入すると \\ \d S&=&\f{nR}{V}\d V \\ このとき&、&まず、Aについて始状態と終状態まで積分すると、 \\ ΔS_A&=&n_AR\ln\f{V_{終状態}}{V_{始状態}} \\ このとき理想気体なので&、&\\ \f{V_{終状態}}{V_{始状態}}&=&\f{n_A+n_B}{n_A} となるので\\ ΔS_A&=& n_AR\ln\f{n_A+n_B}{n_A}\\ となる。&& \\ 同様にして&、&Bの気体の方でも\\ ΔS_B&=& n_BR\ln\f{n_A+n_B}{n_B}\\ となるので&、&混合エントロピーは\\ Δ_{\rm mix}S&=&ΔS_A+ΔS_B \\ &=&n_AR\ln\f{n_A+n_B}{n_A}+n_BR\ln\f{n_A+n_B}{n_B}\\ \end{eqnarray}$$

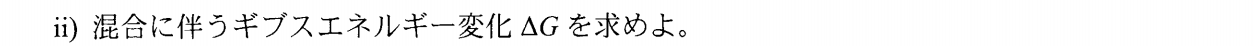$$\begin{eqnarray} Δ_{\rm mix}G&=&Δ_{\rm mix}H-TΔ_{\rm mix}S であり、\\ Δ_{\rm mix}H&=&0なので \\ Δ_{\rm mix}G&=&-TΔ_{\rm mix}S \\ &=&n_ART\ln\f{n_A+n_B}{n_A}+n_BRT\ln\f{n_A+n_B}{n_B}\\ \end{eqnarray}$$

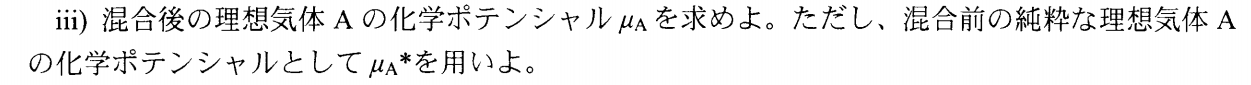
$$\begin{eqnarray} μ_A&=&μ_A*+RT\ln\f{P_A}{P} \\ 混合後のAの分圧P_AはP_A&=&\f{n_ART}{V} より、\\ &&Aの物質量に比例するから\\ μ_A&=&μ_A^*+RT\ln\f{n_A}{n_A+n_B} \\ \end{eqnarray}$$