方位ベクトルの方向に沿って、切り口が方位ベクトルと交わる切片の値をもとに、切り口の面を定義するのが、ミラー指数と呼ばれるものです。
ミラー指数の定義
①結晶の３つの方位ベクトル$a,b,c$の軸（結晶学的方向）と面との交点(切片)の値を見つける。ある軸と平行で交点を持たない場合は∞とする。
②得られた３つの値について、それぞれの逆数を取る。
③その結果に分母の最小公倍数をかけて整数とする。得られた$(h k l)$がMiller指数である。
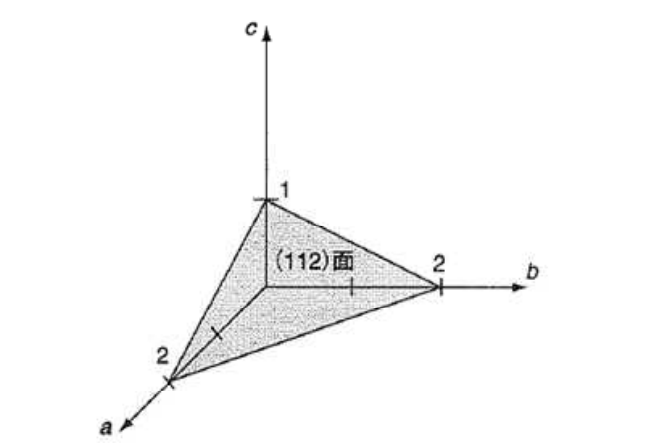
例えば、以上の灰色の面は$a$軸とは$2$,$b$軸とは$2$,c軸とは$1$と交わっています。このような面は、$(112)$面と言われます。まず、
①切片は$(a b c)=(221)$です。
②逆数を取ると、$\s{\f1a\f1b\f1c}=\s{\f12\f121}$です。
③最小公倍数$2$を掛けると、$(hkl)=(112)$となります。
面心立方格子の(100),(110,)(111)が最もシンプルで、代表的なものです。
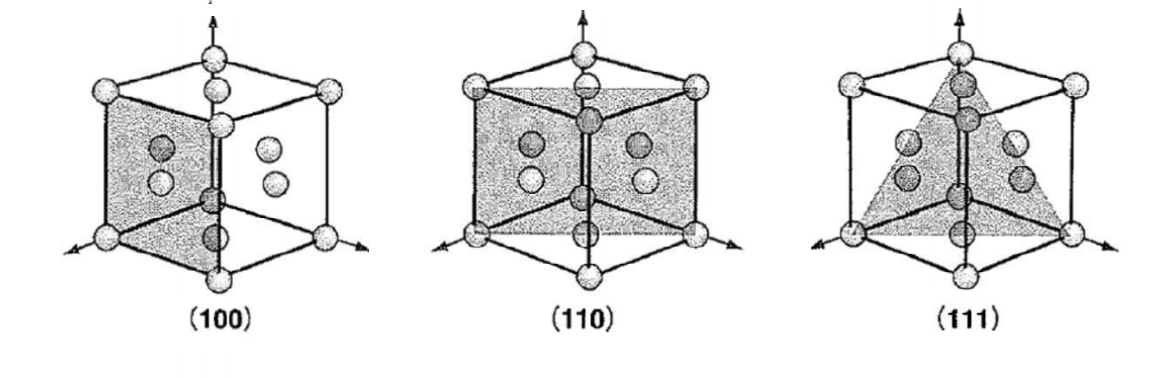
$(100)$では、$a$軸とは$1$で交わりますが、$b,c$軸では交わりません。つまり、切片は$∞$です。よって、その逆数を取るので、$(100)$となります。
$(110)$でも同様です。
$(111)$面というのは、切り口が三角形になっていて、切り口が最も密になっています。つまり安定です。
逆に、$(100)$は隙間が大きいので、$(111)$ほど安定ではありません。隙間が多い表面は安定化する余地があります。
この中で最も表面密度が低いのは$(100)$面です。そのため、表面構造の変化を起こすことが知られています。
同様に体心立方格子についても、
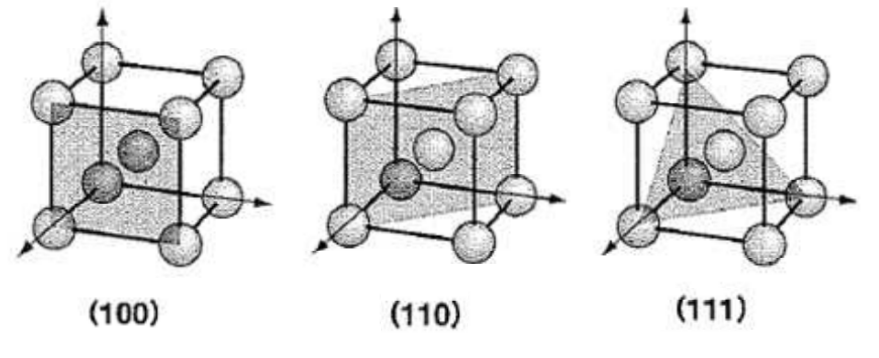となります。ただし、体心立方格子の表面面心立方格子ほどは扱われません。