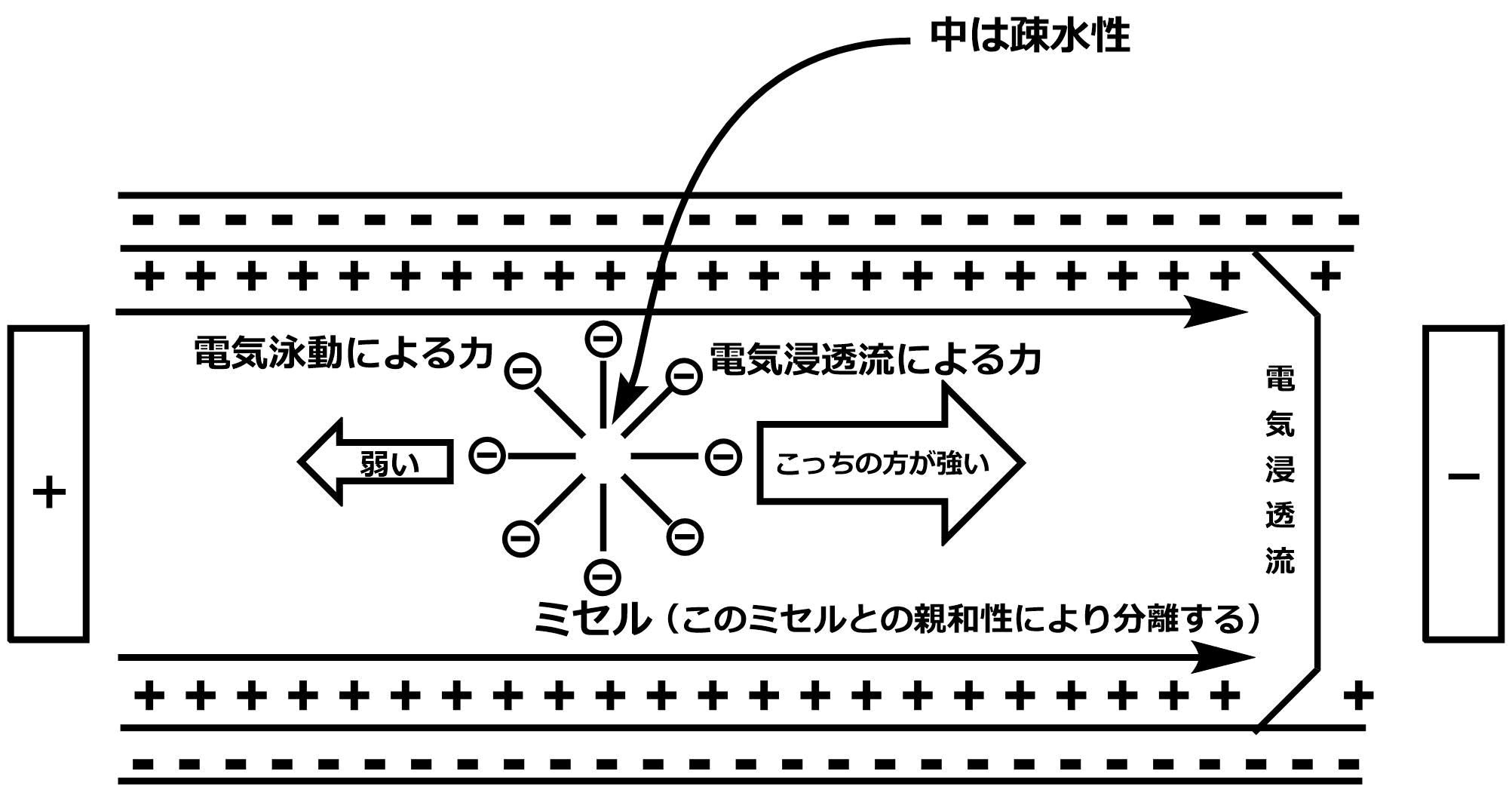
ミセル導電クロマトグラフィーでは緩衝溶液にイオン性ミセルを添加し、電圧をかけていく。このとき、キャピラリーの壁面は緩衝溶液を加えることによりシラノール基($ \rm Si-OH$)のプロトンが解離し、$\rm Si-O^-$という負電荷をもつ状態をとる。そのため、緩衝溶液中の陽イオンが壁面に集まり、電気二重層を形成する。ここに電圧がかかると、壁面に集まった陽イオンが移動を開始し、それによって溶液全体も移動する。つまり、+の電圧がかかっている側から-の電圧がかかっている方向に移動する。これを電気浸透流という。また、界面活性剤は一般的に陰イオンを用いる。そうすると、ミセルを形成したときに外側が負電荷を帯び、中心に疎水基が集まった状態となる。この状態で電圧がかかると、ミセルの表面の負電荷は+の電圧がかかっている方向に引き寄せられる。このとき、ミセルにかかる電気浸透流による力と、電気泳動による力は反対方向を向く。そのため、ミセルは疑似的に固定相としてみなすことができる。(ただ、一般的には電気浸透流の力のほうが電気泳動による力よりも大きいため、最終的にはミセルも溶出することになる)そして、試料溶液中のミセルとの親和性が高い物質ほどミセルに取り込まれやすいことを利用して、分離することができる。この分離法の特徴として、キャピラリー電気泳動では分離できなかった中性物質も分離できることにある。ミセルの中心は疎水性なので、疎水性相互作用により、中性物質は取り込まれやすくなる。さらに、イオン性の物質でもミセルとの相性により分離が可能である。ミセル導電クロマトグラフィーが高分解能を持つ理由は理論段高の高さにある。
クロマトグラフィーは理論段高が小さいほど高分解能であると評価することができる。
理論段高は以下の式で表される。
$$H=A+\f{B}{u}+Cu$$ $u$は流速を表し、$A$は流路の差による分散の項、$B$は移動相中の試料成分の軸方向への拡散の度合いを表す項、$C$は相関物質移動項といい、溶質が移動相と固定相の間を移動する際には2つの相関で達成される平衡に有限な時間が必要であることに由来する項である。ここで、ミセル導電クロマトグラフィーではキャピラリーを用いているので、流路の差$A$は無視できる。また、液体の拡散係数も非常に小さいため、$B$も無視できる。そして、ミセルという小さいスケールの平衡であるため、平衡完了に要する時間は非常に小さく、つまり平衡状態からの差である$C$も無視できる。以上のことより、理論段高が極めて小さくるため、このクロマトグラフィーは高分解能だということができる。
詳しくはファン・デームテルの式にて。